
【题目】如图,在直角坐标系xOy中,圆O:x2+y2=4与x轴负半轴交于点A,过点A的直线AM,AN分别与圆O交于M,N两点,设直线AM、AN的斜率分别为k1、k2.
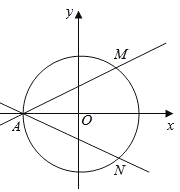
(1)若![]() ,求△AMN的面积;
,求△AMN的面积;
(2)若k1k2=-2,求证:直线MN过定点.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)由题意得到直线AM与AN的方程,利用垂径定理分别求得AM与AN的值,再由两直线垂直,代入三角形面积公式求解;
(2)由题知直线AM的方程y=k1(x+2),直线AN的方程为![]() .分别与圆的方程联立求得M,N的坐标,写出MN的直线方程,利用直线系方程即可证明线MN过定点.
.分别与圆的方程联立求得M,N的坐标,写出MN的直线方程,利用直线系方程即可证明线MN过定点.
(1)由题知,直线AM的方程为y=2x+4,直线AN的方程为![]() .
.
∴圆心到直线AM的距离![]() ,得
,得![]() ,
,
同理求得![]() ,
,
由题知k1k2=-1,得AN⊥AM,
![]() ;
;
(2)由题知直线AM的方程y=k1(x+2),直线AN的方程为![]() .
.
联立方程 ,得
,得![]() ,
,
得x=-2或![]() ,
,
∴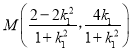 ,同理,
,同理,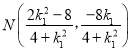 ,
,
∴直线MN为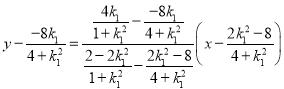 .
.
即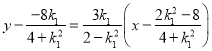 ,得
,得![]() ,
,
∴直线MN恒过定点![]() .
.


科目:高中数学 来源: 题型:
【题目】交强险是车主须为机动车购买的险种.若普通![]() 座以下私家车投保交强险第一年的费用(基本保费)是
座以下私家车投保交强险第一年的费用(基本保费)是![]() 元,在下一年续保时,实行费率浮动制,其保费与上一年度车辆发生道路交通事故情况相联系,具体浮动情况如下表:
元,在下一年续保时,实行费率浮动制,其保费与上一年度车辆发生道路交通事故情况相联系,具体浮动情况如下表:
类型 | 浮动因素 | 浮动比率 |
| 上一年度未发生有责任的道路交通事故 | 下浮 |
| 上两年度未发生有责任的道路交通事故 | 下浮 |
| 上三年度未发生有责任的道路交通事故 | 下浮 |
| 上一年度发生一次有责任不涉及死亡的道路交通事故 |
|
| 上一年度发生两次及以上有责任不涉及死亡的道路交通事故 | 上浮 |
| 上三年度发生有责任涉及死亡的道路交通事故 | 上浮 |
某一机构为了研究某一品牌![]() 座以下投保情况,随机抽取了
座以下投保情况,随机抽取了![]() 辆车龄满三年的该品牌同型号私家车的下一年续保情况,统计得到如下表格:
辆车龄满三年的该品牌同型号私家车的下一年续保情况,统计得到如下表格:
类型 |
|
|
|
|
|
|
数量 |
|
|
|
|
|
|
以这![]() 辆该品牌汽车的投保类型的频率视为概率.
辆该品牌汽车的投保类型的频率视为概率.
(I)试估计该地使用该品牌汽车的一续保人本年度的保费不超过![]() 元的概率;
元的概率;
(II)记![]() 为某家庭的一辆该品牌车在第四年续保时的费用,求
为某家庭的一辆该品牌车在第四年续保时的费用,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(l)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: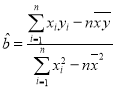 ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《九章算术》中,将底面为直角三角形且侧棱垂直于底面的三棱柱称之为堑堵;将底面为矩形且一侧棱垂直于底面的四棱锥称之为阳马;将四个面均为直角三角形的四面体称之为鳖臑[biē nào].某学校科学小组为了节约材料,拟依托校园内垂直的两面墙和地面搭建一个堑堵形的封闭的实验室![]() ,
,![]() 是边长为2的正方形.
是边长为2的正方形.


(1)若![]() 是等腰三角形,在图2的网格中(每个小方格都是边长为1的正方形)画出堑堵的三视图;
是等腰三角形,在图2的网格中(每个小方格都是边长为1的正方形)画出堑堵的三视图;
(2)若![]() ,
,![]() 在
在![]() 上,证明:
上,证明:![]() ,并回答四面体
,并回答四面体![]() 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
(3)当阳马![]() 的体积最大时,求点
的体积最大时,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下命题:①如果向量![]() 与任何向量不能构成空间向量的一组基底,那么
与任何向量不能构成空间向量的一组基底,那么![]() 的关系是不共线;②
的关系是不共线;②![]() 为空间四点,且向量
为空间四点,且向量![]() 不构成空间的一个基底,那么点
不构成空间的一个基底,那么点![]() 一定共面;③已知向量
一定共面;③已知向量![]() 是空间的一个基底,则向量
是空间的一个基底,则向量![]() ,也是空间的一个基底。其中正确的命题是( )
,也是空间的一个基底。其中正确的命题是( )
A. ①②B. ①③C. ②③D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |
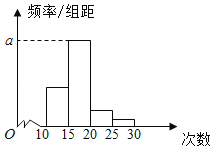
(1)求出表中M,p及图中a的值;
(2)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,请列举出所有基本事件,并求至多1人参加社区服务次数在区间[20,25)内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com