
【题目】随机变量ξ的分布列如表,其中a,b,c成等差数列.若E(ξ)= ![]() ,则D(ξ)=( )
,则D(ξ)=( )
ξ | 1 | 2 | 3 |
P | a | b | c |
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:∵a,b,c成等差数列,E(ξ)= ![]() ,
,
∴由随机变量ξ的分布列的性质得:
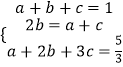 ,
,
解得a= ![]() ,b=
,b= ![]() ,c=
,c= ![]() ,
,
∴D(ξ)=(1﹣ ![]() )2×
)2× ![]() +(2﹣
+(2﹣ ![]() )2×
)2× ![]() +(3﹣
+(3﹣ ![]() )2×
)2× ![]() =
= ![]() .
.
故选:D.
【考点精析】解答此题的关键在于理解离散型随机变量及其分布列的相关知识,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
【题目】某食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系t=![]() 且该食品在4℃的保鲜时间是16小时。已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示。给出以下四个结论:
且该食品在4℃的保鲜时间是16小时。已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示。给出以下四个结论: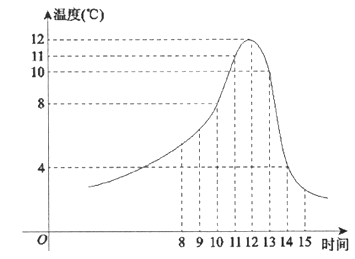
①该食品在6℃的保鲜时间是8小时;
②当x∈[-6,6]时,该食品的保鲜时间t随着x增大而逐渐减少;
③到了此日13时,甲所购买的食品还在保鲜时间内;
④到了此日14时,甲所购买的食品已然过了保鲜时间。
其中,所有正确结论的序号是__________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过点
的图象经过点![]() ,且函数
,且函数![]() =
= ![]() 是偶函数
是偶函数
(1)求![]() 的解析式;
的解析式;
(2)已知![]() ,求函数
,求函数![]() 在
在![]() 的最大值和最小值
的最大值和最小值
(3)函数![]() 的图象上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
的图象上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=![]() ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动. 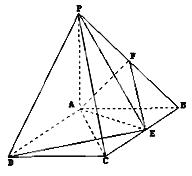
(1)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)证明:无论点E在边BC的何处,都有PE⊥AF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果对定义在R上的函数f(x)对任意两个不相等的实数x1 , x2 , 都有(x1﹣x2)[f(x1)﹣f(x2)]>0,则称函数f(x)为“H函数”.给出下列函数①y=﹣x3+x+1;②y=3x﹣2(sinx﹣cosx);③y=ex+1;④ ![]() .其中“H函数”的个数为( )
.其中“H函数”的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱ABC-A1B1C1中,△ABC与△A1B1C1都为正三角形且AA1⊥面ABC,F、F1分别是AC,A1C1的中点.

求证:(1)平面AB1F1∥平面C1BF;
(2)平面AB1F1⊥平面ACC1A1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别为CD和PC的中点.

求证:(1) BE∥平面PAD;
(2) 平面BEF⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=2sin2ωx+2sinωxcosωx﹣1(ω>0)的周期为π.
(Ⅰ)求ω的值;
(Ⅱ)求函数f(x)在[ ![]() ,
, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com