
【题目】现有4个人去参加娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(1)求这4个人中恰有2人去参加甲游戏的概率;
(2)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(3)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记ξ=|X﹣Y|,求随机变量ξ的分布列与数学期望Eξ.
【答案】
(1)解::依题意,这4个人中,每个人去参加甲游戏的概率为 ![]() ,去参加乙游戏的人数的概率为
,去参加乙游戏的人数的概率为 ![]()
设“这4个人中恰有i人去参加甲游戏”为事件Ai(i=0,1,2,3,4),∴P(Ai)= ![]()
这4个人中恰有2人去参加甲游戏的概率为P(A2)= ![]()
(2)解:设“这4个人中去参加甲游戏的人数大于去参加乙游戏”为事件B,则B=A3∪A4,
∴P(B)=P(A3)+P(A4)= ![]()
(3)解:ξ的所有可能取值为0,2,4,由于A1与A3互斥,A0与A4互斥,故P(ξ=0)=P(A2)= ![]()
P(ξ=2)=P(A1)+P(A3)= ![]() ,P(ξ=4)=P(A0)+P(A4)=
,P(ξ=4)=P(A0)+P(A4)= ![]()
∴ξ的分布列是
ξ | 0 | 2 | 4 |
P |
|
|
|
数学期望Eξ= ![]()
【解析】依题意,这4个人中,每个人去参加甲游戏的概率为 ![]() ,去参加乙游戏的人数的概率为
,去参加乙游戏的人数的概率为 ![]() 设“这4个人中恰有i人去参加甲游戏”为事件Ai(i=0,1,2,3,4),故P(Ai)=
设“这4个人中恰有i人去参加甲游戏”为事件Ai(i=0,1,2,3,4),故P(Ai)= ![]() (1)这4个人中恰有2人去参加甲游戏的概率为P(A2);(2)设“这4个人中去参加甲游戏的人数大于去参加乙游戏”为事件B,则B=A3∪A4 , 利用互斥事件的概率公式可求;(3)ξ的所有可能取值为0,2,4,由于A1与A3互斥,A0与A4互斥,求出相应的概率,可得ξ的分布列与数学期望.
(1)这4个人中恰有2人去参加甲游戏的概率为P(A2);(2)设“这4个人中去参加甲游戏的人数大于去参加乙游戏”为事件B,则B=A3∪A4 , 利用互斥事件的概率公式可求;(3)ξ的所有可能取值为0,2,4,由于A1与A3互斥,A0与A4互斥,求出相应的概率,可得ξ的分布列与数学期望.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】已知点A(2,2),B(3,4),C(m,0),△ABC的面积为5.
(1)求m的值;
(2)若m>0,∠BAC的平分线交线段BC于D,求点D的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() ,g(x)=﹣x﹣ln(﹣x)其中a≠0,
,g(x)=﹣x﹣ln(﹣x)其中a≠0,
(1)若x=1是函数f(x)的极值点,求实数a的值及g(x)的单调区间;
(2)若对任意的x1∈[1,2],x2∈[﹣3,﹣2]使得f(x1)≥g(x2)恒成立,且﹣2<a<0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:对于m∈[﹣1,1],不等式a2﹣5a﹣3≥ ![]() 恒成立;命题q:不等式x2+ax+2<0有解,若p∨q为真,且p∧q为假,求a的取值范围.
恒成立;命题q:不等式x2+ax+2<0有解,若p∨q为真,且p∧q为假,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=lnf′(x)的单调减区间为( ) 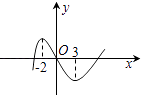
A.[0,3)
B.[﹣2,3]
C.(﹣∞,﹣2)
D.[3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的部分图象如图所示,将y=f(x)的图象向右平移
)的部分图象如图所示,将y=f(x)的图象向右平移 ![]() 个单位长度后得到函数y=g(x)的图象.
个单位长度后得到函数y=g(x)的图象. 
(1)求函数y=g(x)的解析式;
(2)在△ABC中,角A,B,C满足2sin2 ![]() =g(C+
=g(C+ ![]() )+1,且其外接圆的半径R=2,求△ABC的面积的最大值.
)+1,且其外接圆的半径R=2,求△ABC的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)=﹣x2+ax﹣2
(Ⅰ)求函数f(x)在[t,t+2](t>0)上的最小值;
(Ⅱ)若函数y=f(x)与y=g(x)的图象恰有一个公共点,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
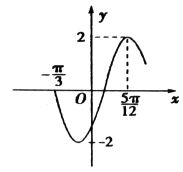
【题目】函数f(x)=Asin(ωx+φ),x∈R,(ω>0,﹣ ![]() <φ<
<φ< ![]() )的部分图象如图所示.
)的部分图象如图所示.
(Ⅰ)确定A,ω,φ的值,并写出函数f(x)的解析式;
(Ⅱ)描述函数y=f(x)的图象可由函数y=sinx的图象经过怎样的变换而得到;
(Ⅲ)若f( ![]() )=
)= ![]() (
( ![]() <α<
<α< ![]() ),求tan2(α﹣
),求tan2(α﹣ ![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com