
����Ŀ��ijѧУ�����꼶��ѧ��1 000���������飬����750��ͬѧ�����μ���������(��ΪA��ͬѧ)������250��ͬѧ�������μ���������(��ΪB��ͬѧ)�����÷ֲ��������(��A�ࡢB�������)�Ӹ��꼶��ѧ���й����100��ͬѧ����������ߴ�165 cm��Ϊ���ı����Գ�ȡ��100��ѧ�����õ�������������
���ߴ�� | ���߲���� | �ܼ� | |
������������� | 40 | ||
��������������� | 15 | ||
�ܼ� | 100 |
��1������ϱ���
��2���ܷ��ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ�����μ��������������ߴ���й�ϵ(K2�Ĺ۲�ֵ��ȷ��0.001)?
���𰸡�
��1���⣺��д���������£�
���ߴ�� | ���߲���� | �ܼ� | |
������������� | 40 | 35 | 75 |
��������������� | 10 | 15 | 25 |
�ܼ� | 50 | 50 | 100 |
��2���⣺���������е����ݣ���K 2�Ĺ۲�ֵΪ
![]()
���Բ����ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ�����μ��������������ߴ���й�ϵ��
����������1�����������֪��ȡ��ѧ���о����μ�����������ѧ��Ϊ75�ˣ��������μ�����������ѧ��Ϊ25�ˣ��Ӷ�����ɱ���2�����ݣ�1���еı���K�Ĺ�ʽ��ֵ�����ó�����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P�dz��᳤Ϊ ![]() ����ԲQ��
����ԲQ�� ![]() �����ڶ����һ�����㣬OΪ����ԭ�㣬AΪ��Բ���Ҷ��㣬��MΪ�߶�PA���е㣬��ֱ��PA��OM��б��֮����Ϊ
�����ڶ����һ�����㣬OΪ����ԭ�㣬AΪ��Բ���Ҷ��㣬��MΪ�߶�PA���е㣬��ֱ��PA��OM��б��֮����Ϊ ![]() ��
��
��1������ԲQ�ķ��̣�
��2�������F1�Ҳ��������ᴹֱ��ֱ��l����Բ��C��D���㣬�߶�CD�Ĵ�ֱƽ������x�ύ�ڵ�G����G�������ȡֵ��Χ�� ![]() ����|CD|����Сֵ��
����|CD|����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ֱ������ϵ ![]() �У�ֱ��
�У�ֱ�� ![]() �IJ�������Ϊ
�IJ�������Ϊ ![]() ��
�� ![]() Ϊ����������ԭ��Ϊ���㣬
Ϊ����������ԭ��Ϊ���㣬 ![]() ��������Ϊ���Ὠ��������ϵ��Բ
��������Ϊ���Ὠ��������ϵ��Բ ![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ ![]() .
.
��1��д��ֱ�� ![]() ����ͨ���̼�Բ
����ͨ���̼�Բ ![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2���� ![]() ��ֱ��
��ֱ�� ![]() �ϵĵ㣬���
�ϵĵ㣬��� ![]() �����꣬ʹ
�����꣬ʹ ![]() ��Բ��
��Բ�� ![]() �ľ�����С.
�ľ�����С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������ĵȱ�����![]() ����
����![]() ,��
,��![]() ��
��![]() �ĵȲ�����.
�ĵȲ�����.
(��)������![]() ��ͨ�ʽ��
��ͨ�ʽ��
(��)��![]() ,������������
,������������![]() ��
�� ![]() �����������
�����������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�洬�ں����в������գ����������źţ��Һ�����ͧ��![]() ����Ϥ������������洬�ڷ�λ�ǣ���ָ������˳ʱ��ת��Ŀ�귽���ߵ�ˮƽ�ǣ�Ϊ
����Ϥ������������洬�ڷ�λ�ǣ���ָ������˳ʱ��ת��Ŀ�귽���ߵ�ˮƽ�ǣ�Ϊ![]() ������Ϊ15�����
������Ϊ15�����![]() ����������洬���ط�λ��Ϊ
����������洬���ط�λ��Ϊ![]() �ķ�����15����/Сʱ���ٶ���С��
�ķ�����15����/Сʱ���ٶ���С��![]() ��£���Һ�����ͧ������
��£���Һ�����ͧ������![]() ����/Сʱ���ٶ�ǰȥӪ�ȣ���ͧ�����洬���������ʱ��ͽ�ͧ�ĺ���.
����/Сʱ���ٶ�ǰȥӪ�ȣ���ͧ�����洬���������ʱ��ͽ�ͧ�ĺ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ�����ڶ�ͬһ��� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ���������Ʒ��ֻ��һ��һ�Ƚ�������������ǰ���ס��ҡ���������λͬѧ�������������ƷԤ�����£�
���������Ʒ��ֻ��һ��һ�Ƚ�������������ǰ���ס��ҡ���������λͬѧ�������������ƷԤ�����£�
��˵������ ![]() ��
�� ![]() ��Ʒ���һ�Ƚ�����
��Ʒ���һ�Ƚ�����
��˵���� ![]() ��Ʒ���һ�Ƚ�����
��Ʒ���һ�Ƚ�����
��˵���� ![]() ��
�� ![]() ������Ʒδ���һ�Ƚ�����
������Ʒδ���һ�Ƚ�����
��˵������ ![]() ��Ʒ���һ�Ƚ���.
��Ʒ���һ�Ƚ���.
������λͬѧ��ֻ����λ˵�Ļ��ǶԵģ�����һ�Ƚ�����Ʒ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊ�˽�ij�����õ����������˸���100�������¾��õ�������λ��![]() ����
����![]() �����Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.
�����Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.
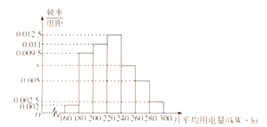
(1)���������¾��õ���Ϊ![]() ���û�������
���û�������
(2)�����¾��õ�������λ����
(3)���¾��õ���Ϊ![]() �������û��У��÷ֲ�����ķ�����ȡ22���������¾��õ���Ϊ
�������û��У��÷ֲ�����ķ�����ȡ22���������¾��õ���Ϊ![]() ���û���Ӧ�ó�ȡ���ٻ���
���û���Ӧ�ó�ȡ���ٻ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˫���� ![]() ��a��0��b��0������ΪF1 �� ��ΪA����F1��x��Ĵ��߽�˫������P��Q���㣬��P��PM��ֱQA��M����Q��QN��ֱPA��N����PM��QN�Ľ���ΪB����B��ֱ��PQ�ľ������a+
��a��0��b��0������ΪF1 �� ��ΪA����F1��x��Ĵ��߽�˫������P��Q���㣬��P��PM��ֱQA��M����Q��QN��ֱPA��N����PM��QN�Ľ���ΪB����B��ֱ��PQ�ľ������a+ ![]() �����˫���ߵ�������ȡֵ��Χ�ǣ� ��
�����˫���ߵ�������ȡֵ��Χ�ǣ� ��
A.��1�� ![]() ��
��
B.�� ![]() ��+�ޣ�
��+�ޣ�
C.��1��2 ![]() ��
��
D.��2 ![]() ��+�ޣ�
��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
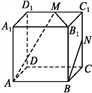
����Ŀ����ͼ��ʾ,��������ABCD-A1B1C1D1��,M,N�ֱ�Ϊ��C1D1,C1C���е�,�������ĸ�����:
��ֱ��AM��CC1���ֱཻ��;��ֱ��AM��BN��ƽ��ֱ��;
��ֱ��BN��MB1������ֱ��; ��ֱ��MN��AC���ɵĽ�Ϊ60��.
������ȷ�Ľ���Ϊ___����(ע:������Ϊ��ȷ�Ľ�����Ŷ�����).
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com