
【题目】要得到y= ![]() cos2x+sinxcosx的图象,只需把y=sin2x的图象上所有点( )
cos2x+sinxcosx的图象,只需把y=sin2x的图象上所有点( )
A.向左平移 ![]() 个单位,再向上移动
个单位,再向上移动 ![]() 个单位
个单位
B.向左平移 ![]() 个单位,再向上移动
个单位,再向上移动 ![]() 个单位
个单位
C.向右平移 ![]() 个单位,再向下移动
个单位,再向下移动 ![]() 个单位
个单位
D.向右平移 ![]() 个单位,再向下移动
个单位,再向下移动 ![]() 个单位
个单位
科目:高中数学 来源: 题型:
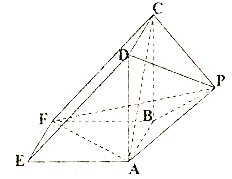
【题目】如图所示,该几何体是由一个直三棱柱![]() 和一个正四棱锥
和一个正四棱锥![]() 组合而成,
组合而成,![]() ,
,![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求正四棱锥![]() 的高
的高![]() ,使得该四棱锥的体积是三棱锥
,使得该四棱锥的体积是三棱锥![]() 体积的4倍.
体积的4倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,其反函数为y=g(x).
,其反函数为y=g(x).
(1)若g(mx2+2x+1)的定义域为R,求实数m的取值范围;
(2)当x∈[﹣1,1]时,求函数y=[f(x)]2﹣2af(x)+3的最小值h(a);
(3)是否存在实数m>n>2,使得函数y=h(x)的定义域为[n,m],值域为[n2 , m2],若存在,求出m、n的值;若不存在,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos2 ![]() +
+ ![]() sinωx﹣
sinωx﹣ ![]() (ω>0),x∈R,若f(x)在区间(π,2π)内没有零点,则ω的取值范围是( )
(ω>0),x∈R,若f(x)在区间(π,2π)内没有零点,则ω的取值范围是( )
A.(0, ![]() ]
]
B.(0, ![]() ]∪[
]∪[ ![]() ,
, ![]() )
)
C.(0, ![]() ]
]
D.(0, ![]() ]∪[
]∪[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() +cos2x+a(a∈R,a为常数). (Ⅰ)求函数的最小正周期;
+cos2x+a(a∈R,a为常数). (Ⅰ)求函数的最小正周期;
(Ⅱ)求函数的单调递减区间;
(Ⅲ)若 ![]() 时,f(x)的最小值为﹣2,求a的值.
时,f(x)的最小值为﹣2,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有一批专业技术人员,对他们进行年龄状况和接受教育程度(学历)的调查,其结果(人数分布)如表:
学历 | 35岁以下 | 35~50岁 | 50岁以上 |
本科 | 80 | 30 | 20 |
研究生 | x | 20 | y |
(Ⅰ)用分层抽样的方法在35~50岁年龄段的专业技术人员中抽取一个容量为10的样本,将该样本看成一个总体,从中任取3人,求至少有1人的学历为研究生的概率;
(Ⅱ)在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取N个人,其中35岁以下48人,50岁以上10人,再从这N个人中随机抽取出1人,此人的年龄为50岁以上的概率为 ![]() ,求x、y的值.
,求x、y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com