
【题目】 如图,在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形,![]() 为等边三角形,平面
为等边三角形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,
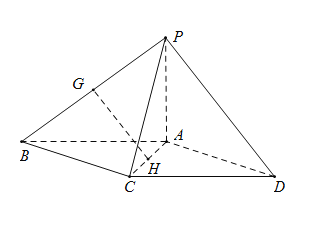
(Ⅰ)设![]() 分别为
分别为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(I)见解析;(II)见解析;(III)![]() .
.
【解析】
(I)连接![]() ,结合平行四边形的性质,以及三角形中位线的性质,得到
,结合平行四边形的性质,以及三角形中位线的性质,得到![]() ,利用线面平行的判定定理证得结果;
,利用线面平行的判定定理证得结果;
(II)取棱![]() 的中点
的中点![]() ,连接
,连接![]() ,依题意,得
,依题意,得![]() ,结合面面垂直的性质以及线面垂直的性质得到
,结合面面垂直的性质以及线面垂直的性质得到![]() ,利用线面垂直的判定定理证得结果;
,利用线面垂直的判定定理证得结果;
(III)利用线面角的平面角的定义得到![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,放在直角三角形中求得结果.
所成的角,放在直角三角形中求得结果.
(I)证明:连接![]() ,易知
,易知![]() ,
,![]() ,
,
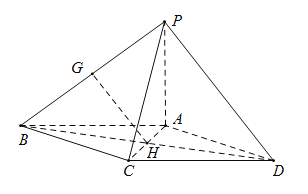
又由![]() ,故
,故![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(II)证明:取棱![]() 的中点
的中点![]() ,连接
,连接![]() ,依题意,得
,依题意,得![]() ,
,
又因为平面![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,故
,故![]() ,
,
又已知![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
(III)解:连接![]() ,由(II)中
,由(II)中![]() 平面
平面![]() ,
,
可知![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.
所成的角.
因为![]() 为等边三角形,
为等边三角形,![]() 且
且![]() 为
为![]() 的中点,
的中点,
所以![]() ,又
,又![]() ,
,
在![]() 中,
中,![]() ,
,
所以,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某客户准备在家中安装一套净水系统,该系统为二级过滤,使用寿命为十年如图所示两个二级过滤器采用并联安装,再与一级过滤器串联安装.

其中每一级过滤都由核心部件滤芯来实现在使用过程中,一级滤芯和二级滤芯都需要不定期更换(每个滤芯是否需要更换相互独立).若客户在安装净水系统的同时购买滤芯,则一级滤芯每个160元,二级滤芯每个80元.若客户在使用过程中单独购买滤芯则一级滤芯每个400元,二级滤芯每个200元.现需决策安装净水系统的同时购买滤芯的数量,为此参考了根据100套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中表1是根据100个一级过滤器更换的滤芯个数制成的频数分布表,图2是根据200个二级过滤器更换的滤芯个数制成的条形图.
表1:一级滤芯更换频数分布表
一级滤芯更换的个数 | 8 | 9 |
频数 | 60 | 40 |
图2:二级滤芯更换频数条形图

以100个一级过滤器更换滤芯的频率代替1个一级过滤器更换滤芯发生的概率,以200个二级过滤器更换滤芯的频率代替1个二级过滤器更换滤芯发生的概率.
(1)求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为16的概率;
(2)记![]() 表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求
表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)记![]() 分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若
分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若![]() ,且
,且![]() ,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定
,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从抛物线![]() 上任意一点
上任意一点![]() 向
向![]() 轴作垂线段垂足为
轴作垂线段垂足为![]() ,点
,点![]() 是线段
是线段![]() 上的一点,且满足
上的一点,且满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 两点,点
两点,点![]() 为轨迹
为轨迹![]() 上异于
上异于![]() 的任意一点,直线
的任意一点,直线![]() 分别与直线
分别与直线![]() 交于
交于![]() 两点.问:
两点.问:![]() 轴正半轴上是否存在定点使得以
轴正半轴上是否存在定点使得以![]() 为直径的圆过该定点?若存在,求出符合条件的定点坐标;若不存在,请说明理由.
为直径的圆过该定点?若存在,求出符合条件的定点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方形![]() 的边长为
的边长为![]() ,已知
,已知![]() ,将
,将![]() 沿
沿![]() 边折起,折起后
边折起,折起后![]() 点在平面
点在平面![]() 上的射影为
上的射影为![]() 点,则翻折后的几何体中有如下描述:①
点,则翻折后的几何体中有如下描述:①![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ;②
;②![]() ;③
;③![]() ;④平面
;④平面![]() 平面
平面![]() ,其中正确的命题序号为___________.
,其中正确的命题序号为___________.
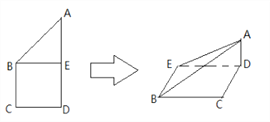
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.

(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱台![]() 中,点
中,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 是
是![]() 内(含边界)的一个动点,且有平面
内(含边界)的一个动点,且有平面![]() 平面
平面![]() ,则动点
,则动点![]() 的轨迹是( )
的轨迹是( )

A. 平面B. 直线C. 线段,但只含1个端点D. 圆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S-ABC中,∠ABC=90°,D是AC的中点,且SA=SB=SC.
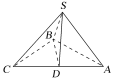
(1)求证:SD⊥平面ABC;
(2)若AB=BC,求证:BD⊥平面SAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,a1+2a2+3a3+…+nan=![]() (n∈N*)
(n∈N*)
(Ⅰ)证明当n≥2时,数列{nan}是等比数列,并求数列{an}的通项an;
(Ⅱ)求数列{n2an}的前n项和Tn;
(Ⅲ)对任意n∈N*,使得![]() 恒成立,求实数λ的最小值.
恒成立,求实数λ的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com