
在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1.
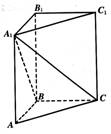
(1)求异面直线B1C1与AC所成角的大小;
(2)若该直三棱柱ABC-A1B1C1的体积为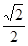 ,求点A到平面A1BC的距离.
,求点A到平面A1BC的距离.
(1)45°;(2)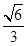 .
.
【解析】
试题分析:(1)求异面直线所成的角,关键是作出这两条直线所成的角,作法是利用平移思想(即作平行线),当然我们要充分利用图中已有的平行关系作图,如本题中有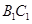 ∥
∥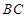 ,就不需要另外作平行线了,还要注意的是异面直线所成的角不大于90°;(2)求点到平面的距离,一般要作出垂线段,求垂线段的长,即过点
,就不需要另外作平行线了,还要注意的是异面直线所成的角不大于90°;(2)求点到平面的距离,一般要作出垂线段,求垂线段的长,即过点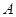 作平面
作平面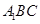 的垂线,首先观察寻找原有图形中的垂直关系,发现可证平面
的垂线,首先观察寻找原有图形中的垂直关系,发现可证平面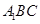 ⊥平面
⊥平面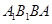 ,因此我们只要在平面
,因此我们只要在平面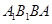 内作
内作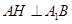 ,垂足为
,垂足为 ,则可证
,则可证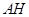 为所要求的垂线段,其长即为要求的距离.另外由于点
为所要求的垂线段,其长即为要求的距离.另外由于点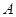 ,平面
,平面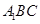 所在的三棱锥
所在的三棱锥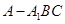 的体积很容易求得,故也可用体积法求解.
的体积很容易求得,故也可用体积法求解.
试题解析:(1)∵BC∥B1C1,
∴∠ACB为异面直线B1C1与AC所成角(或它的补角),(2分)
∵∠ABC=90°,AB=BC=1,
∴∠ACB=45°,
∴异面直线B1C1与AC所成角为45°.(4分)
(2)∵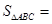
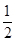 ,三棱柱
,三棱柱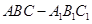 的体积
的体积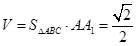 .
.
∴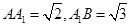 ,(2分)
,(2分)
∵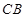 ⊥平面
⊥平面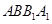 1,∴
1,∴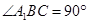 ,
,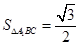 ,
,
设点A到平面A1BC的距离为h,(4分)
三棱锥A1-ABC的体积V=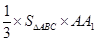 =三棱锥A-A1BC的体积V=
=三棱锥A-A1BC的体积V=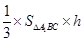 ,(6分)
,(6分)
∴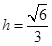 .(8分)
.(8分)
考点:(1)异面直线所成的角;(2)点到平面的距离.


科目:高中数学 来源: 题型:
 如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点.
如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数).
如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数).查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角.
如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,
如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com