
【题目】已知点A(1,2),B(﹣3,﹣1),若圆x2+y2=r2(r>0)上恰有两点M,N,使得△MAB和△NAB的面积均为5,则r的取值范围是 .
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知cosB= ![]() ,tanC=
,tanC= ![]() . (Ⅰ)求tanB和tanA;
. (Ⅰ)求tanB和tanA;
(Ⅱ)若c=1,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的减函数,其导函数f′(x)满足 ![]() +x<1,则下列结论正确的是( )
+x<1,则下列结论正确的是( )
A.对于任意x∈R,f(x)<0
B.对于任意x∈R,f(x)>0
C.当且仅当x∈(﹣∞,1),f(x)<0
D.当且仅当x∈(1,+∞),f(x)>0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+ ![]() ,其中a为大于零的常数..
,其中a为大于零的常数..
(1)若函数f(x)在区间[1,+∞)内单调递增,求a的取值范围;
(2)求函数f(x)在区间[1,2]上的最小值;
(3)求证:对于任意的n∈N* , 且n>1时,都有lnn> ![]() +
+ ![]() +…+
+…+ ![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知双曲线 ![]() =1(a>0,b>0)的左右焦点分别为F1 , F2 , |F1F2|=4,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( )
=1(a>0,b>0)的左右焦点分别为F1 , F2 , |F1F2|=4,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( ) 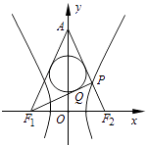
A.3
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平行四边形ABCD的三个顶点的坐标为A(﹣1,5),B(﹣2,﹣1),C(2,3).
(1)求平行四边形ABCD的顶点D的坐标;
(2)在△ACD中,求CD边上的高所在直线方程;
(3)求四边形ABCD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点O为△ABC的外心,角A,B,C的对边分别满足a,b,c, (Ⅰ)若3 ![]() +4
+4 ![]() +5
+5 ![]() =
= ![]() ,求cos∠BOC的值;
,求cos∠BOC的值;
(Ⅱ)若 ![]()
![]() =
= ![]()
![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com