
ЁОЬтФПЁПгаШЫЗЂЯжЃЌЖрПДЕчЪгШнвзЪЙШЫБфРфФЎЃЌШчБэЪЧвЛИіЕїВщЛњЙЙЖдДЫЯжЯѓЕФЕїВщНсЙћЃК
РфФЎ | ВЛРфФЎ | змМЦ | |
ЖрПДЕчЪг | 68 | 42 | 110 |
ЩйПДЕчЪг | 20 | 38 | 58 |
змМЦ | 88 | 80 | 168 |
PЃЈK2ЁнkЃЉ | 0.025 | 0.010 | 0.005 | 0.001 |
k | 5.024 | 6.635 | 7.879 | 10.828 |
K2= ![]() Ёж11.377ЃЌЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
Ёж11.377ЃЌЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
A.ДѓдМга99.9%ЕФАбЮеШЯЮЊЁАЖрПДЕчЪггыШЫБфРфФЎЁБгаЙиЯЕ
B.ДѓдМга99.9%ЕФАбЮеШЯЮЊЁАЖрПДЕчЪггыШЫБфРфФЎЁБУЛгаЙиЯЕ
C.ФГШЫАЎПДЕчЪгЃЌдђЫћБфРфФЎЕФПЩФмадЮЊ99.9%
D.АЎПДЕчЪгЕФШЫжаДѓдМга99.9%ЛсБфРфФЎ
 ФЯДѓНЬИЈЧРЯШЦ№ХмЪюМйЯЮНгНЬГЬФЯОЉДѓбЇГіАцЩчЯЕСаД№АИ
ФЯДѓНЬИЈЧРЯШЦ№ХмЪюМйЯЮНгНЬГЬФЯОЉДѓбЇГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигкКЏЪ§fЃЈxЃЉ=lg ![]() ЃЈxЁй0ЃЌxЁЪRЃЉгаЯТСаУќЬтЃК
ЃЈxЁй0ЃЌxЁЪRЃЉгаЯТСаУќЬтЃК
ЂйКЏЪ§y=fЃЈxЃЉЕФЭМЯѓЙигкyжсЖдГЦЃЛ
ЂкдкЧјМфЃЈЉЁоЃЌ0ЃЉЩЯЃЌКЏЪ§y=fЃЈxЃЉЪЧМѕКЏЪ§ЃЛ
ЂлКЏЪ§fЃЈxЃЉЕФзюаЁжЕЮЊlg2ЃЛ
ЂмдкЧјМфЃЈ1ЃЌ+ЁоЃЉЩЯЃЌКЏЪ§fЃЈxЃЉЪЧдіКЏЪ§ЃЎ
Цфжае§ШЗУќЬтађКХЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4-4ЃКзјБъЯЕгыВЮЪ§ЗНГЬ
вдзјБъдЕу![]() ЮЊМЋЕуЃЌвд
ЮЊМЋЕуЃЌвд![]() жсе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌСНжжзјБъЯЕжаШЁЯрЭЌЕФГЄЖШЕЅЮЛЃЌжБЯп
жсе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌСНжжзјБъЯЕжаШЁЯрЭЌЕФГЄЖШЕЅЮЛЃЌжБЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ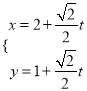 ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌдВ
ЮЊВЮЪ§ЃЉЃЌдВ![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓжБЯп![]() ЕФЦеЭЈЗНГЬгыдВ
ЕФЦеЭЈЗНГЬгыдВ![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉЩшдВ![]() гыжБЯп
гыжБЯп![]() НЛгк
НЛгк![]() СНЕуЃЌШєЕу
СНЕуЃЌШєЕу![]() ЕФжБНЧзјБъЮЊ
ЕФжБНЧзјБъЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП20УћбЇЩњФГДЮЪ§бЇПМЪдГЩМЈЃЈЕЅЮЛЃКЗжЃЉЕФЦЕТЪЗжВМжБЗНЭМШчЭМЃК 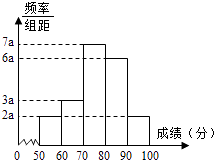
ЃЈ1ЃЉЧѓЦЕТЪЗжВМжБЗНЭМжаaЕФжЕЃЛ
ЃЈ2ЃЉЗжБ№ЧѓГіГЩМЈТфдк[50ЃЌ60ЃЉгы[60ЃЌ70ЃЉжаЕФбЇЩњШЫЪ§ЃЛ
ЃЈ3ЃЉДгГЩМЈдк[50ЃЌ70ЃЉЕФбЇЩњШЮбЁ2ШЫЃЌЧѓДЫ2ШЫЕФГЩМЈЖМдк[60ЃЌ70ЃЉжаЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=exЉ1ЉxЃЎ
ЃЈ1ЃЉШєДцдкxЁЪ[Љ1ЃЌln ![]() ]ЃЌТњзуaЉex+1+xЃМ0ГЩСЂЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
]ЃЌТњзуaЉex+1+xЃМ0ГЩСЂЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
ЃЈ2ЃЉЕБxЁн0ЪБЃЌfЃЈxЃЉЁнЃЈtЉ1ЃЉxКуГЩСЂЃЌЧѓЪЕЪ§tЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєКЏЪ§fЃЈxЃЉЮЊЖЈвхдкRЩЯЕФЦцКЏЪ§ЃЌЧвдкЃЈ0ЃЌ+ЁоЃЉФкЪЧдіКЏЪ§ЃЌгжfЃЈ2ЃЉ=0ЃЌдђВЛЕШЪНx5fЃЈxЃЉЃО0ЕФНтМЏЮЊЃЈ ЃЉ
A.ЃЈЉ2ЃЌ0ЃЉЁШЃЈ2ЃЌ+ЁоЃЉ
B.ЃЈЉЁоЃЌЉ2ЃЉЁШЃЈ0ЃЌ2ЃЉ
C.ЃЈЉ2ЃЌ0ЃЉЁШЃЈ0ЃЌ2ЃЉ
D.ЃЈЉЁоЃЌЉ2ЃЉЁШЃЈ2ЃЌ+ЁоЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕЅЮЛзщжЏжАЙЄШЅФГЕиВЮЙлбЇЯАЃЌашАќГЕЧАЭљЃЌМзГЕЖгЫЕЃКЁАШчЙћСьЖгТђвЛеХШЋЦБЃЌЦфгрШЫПЩЯэЪм7елгХЛнЁЃЁБввГЕЖгЫЕЃКЁАФуУЧЪєгкЭХЬхЦБЃЌАДдМлЕФ7.5елгХЛнЁЃЁБетСНИіГЕЖгЕФдМлЁЂГЕаЭЖМЪЧвЛбљЕФЃЌЪдИљОнЕЅЮЛШЅЕФШЫЪ§БШНЯСНГЕЖгЕФЪеЗбФФМвИќгХЛнЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙВЯэЕЅГЕЪЧжИЦѓвЕдкаЃдАЁЂЕиЬњеОЕуЁЂЙЋНЛеОЕуЁЂОгУёЧјЁЂЩЬвЕЧјЁЂЙЋЙВЗўЮёЧјЕШЬсЙЉздааГЕЕЅГЕЙВЯэЗўЮёЃЌЪЧЙВЯэОМУЕФвЛжжаТаЮЬЌЃЌвЛИіЙВЯэЕЅГЕЦѓвЕдкФГИіГЧЪаОЭЁАвЛЬьжавЛСОЕЅГЕЕФЦНОљГЩБОЃЈЕЅЮЛЃКдЊЃЉгызтгУЕЅГЕЕФЪ§СПЃЈЕЅЮЛЃКГЕСОЃЉжЎМфЕФЙиЯЕЁБНјааЕїВщбаОПЃЌдкЕїВщЙ§ГЬжаНјааСЫЭГМЦЃЌЕУГіЯрЙиЪ§ОнМћЯТБэЃК
зтгУЕЅГЕЪ§СП | 2 | 3 | 4 | 5 | 8 |
УПЬьвЛСОГЕЦНОљГЩБО | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
ИљОнвдЩЯЪ§ОнЃЌбаОПШЫдБЗжБ№НшжњМзЁЂввСНжжВЛЭЌЕФЛиЙщФЃаЭЃЌЕУЕНСНИіЛиЙщЗНГЬЃЌЗНГЬМзЃК ![]() ЃЌЗНГЬввЃК
ЃЌЗНГЬввЃК ![]() .
.
ЃЈ1ЃЉЮЊСЫЦРМлСНжжФЃаЭЕФФтКЯаЇЙћЃЌЭъГЩвдЯТШЮЮёЃК
ЂйЭъГЩЯТБэЃЈМЦЫуНсЙћОЋШЗЕН0.1ЃЉЃЈБИзЂЃК ![]() ЃЌ
ЃЌ ![]() ГЦЮЊЯргІгкЕу
ГЦЮЊЯргІгкЕу![]() ЕФВаВюЃЈвВНаЫцЛњЮѓВюЃЉЃЉЃЛ
ЕФВаВюЃЈвВНаЫцЛњЮѓВюЃЉЃЉЃЛ
зтгУЕЅГЕЪ§СП | 2 | 3 | 4 | 5 | 8 | |
УПЬьвЛСОГЕЦНОљГЩБО | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
ФЃаЭМз | ЙРМЦжЕ | 2.4 | 2.1 | 1.6 | ||
ВаВю | 0 |
| 0.1 | |||
ФЃаЭвв | ЙРМЦжЕ | 2.3 | 2 | 1.9 | ||
ВаВю | 0.1 | 0 | 0 | |||
ЂкЗжБ№МЦЫуФЃаЭМзгыФЃаЭввЕФВаВюЦНЗНКЭ![]() МА
МА![]() ЃЌВЂЭЈЙ§БШНЯ
ЃЌВЂЭЈЙ§БШНЯ![]() ЃЌ
ЃЌ ![]() ЕФДѓаЁЃЌХаЖЯФФИіФЃаЭФтКЯаЇЙћИќКУ.
ЕФДѓаЁЃЌХаЖЯФФИіФЃаЭФтКЯаЇЙћИќКУ.
ЃЈ2ЃЉетИіЙЋЫОдкИУГЧЪаЭЖЗХЙВЯэЕЅГЕКѓЃЌЪмЕНЙуДѓЪаУёЕФШШСвЛЖгЃЌЙВЯэЕЅГЕГЃГЃЙЉВЛгІЧѓЃЌгкЪЧИУЙЋЫОбаОПЪЧЗёдіМгЭЖЗХЃЌИљОнЪаГЁЕїВщЃЌетИіГЧЪаЭЖЗХ8ЧЇСОЪБЃЌИУЙЋЫОЦНОљвЛСОЕЅГЕвЛЬьФмЪеШы10дЊЃЌ6дЊЪеШыЕФИХТЪЗжБ№ЮЊ0.6ЃЌ0.4ЃЛЭЖЗХ1ЭђСОЪБЃЌИУЙЋЫОЦНОљвЛСОЕЅГЕвЛЬьФмЪеШы10дЊЃЌ6дЊЪеШыЕФИХТЪЗжБ№ЮЊ0.4ЃЌ0.6ЃЌЮЪИУЙЋЫОгІИУЭЖЗХ8ЧЇСОЛЙЪЧ1ЭђСОФмЛёЕУИќЖрРћШѓЃПЃЈАДЃЈ1ЃЉжаФтКЯаЇЙћНЯКУЕФФЃаЭМЦЫувЛЬьжавЛСОЕЅГЕЕФЦНОљГЩБОЃЌРћШѓЃНЪеШыЁЊГЩБОЃЉ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИљОнЁА2015ФъЙњУёОМУКЭЩчЛсЗЂеЙЭГМЦЙЋБЈЁБ жаЙЋВМЕФЪ§ОнЃЌДг2011 ФъЕН2015 ФъЃЌЮвЙњЕФ
ЕкШ§ВњвЕдк![]() жаЕФБШжиШчЯТ:
жаЕФБШжиШчЯТ:
ФъЗн |
|
|
|
|
|
ФъЗнДњТы |
|
|
|
|
|
ЕкШ§ВњвЕБШжи |
|
|
|
|
|
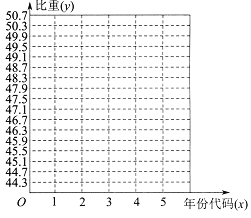
ЃЈ1ЃЉдкЫљИјзјБъЯЕжазїГіЪ§ОнЖдгІЕФЩЂЕуЭМЃЛ
ЃЈ2ЃЉНЈСЂЕкШ§ВњвЕдк![]() жаЕФБШжи
жаЕФБШжи![]() ЙигкФъЗнДњТы
ЙигкФъЗнДњТы![]() ЕФЛиЙщЗНГЬЃЛ
ЕФЛиЙщЗНГЬЃЛ
ЃЈ3ЃЉАДееЕБЧАЕФБфЛЏЧїЪЦЃЌдЄВт2017 ФъЮвЙњЕкШ§ВњвЕдк![]() жаЕФБШжи.
жаЕФБШжи.
ИНзЂ: ЛиЙщжБЯпЗНГЬ![]() жаЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЙЋЪНЗжБ№ЮЊ:
жаЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЙЋЪНЗжБ№ЮЊ:
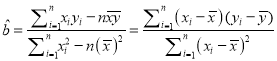 ,
, ![]() .
.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com