
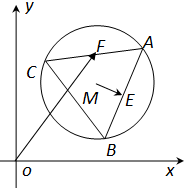
 如图,已知圆M:(x-3)2+(y-3)2=4,△ABC为圆M的内接正三角形,E为边AB的中点,当正△ABC绕圆心M转动,且F是AC边上的中点,
如图,已知圆M:(x-3)2+(y-3)2=4,△ABC为圆M的内接正三角形,E为边AB的中点,当正△ABC绕圆心M转动,且F是AC边上的中点,| ME |
| OF |
| ME |
| OF |
| 1 |
| 2 |
| ME |
| MO |
| OF |
| OM |
| MF |
| ME |
| OF |
| ME |
| OM |
| MF |
| ME |
| OM |
| ME |
| MF |
| ME |
| MF |
| ME |
| MF |
| 1 |
| 2 |
| 1 |
| 2 |
| ME |
| OF |
| 1 |
| 2 |
| ME |
| OM |
| 1 |
| 2 |
| ME |
| MO |
| 2 |
| ME |
| MO |
| 2 |
| ME |
| MO |
| 2 |
| 2 |
| ME |
| OF |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:
| x |
| a |
| x |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 3 |
| 3 |
| π |
| 2 |
| 2π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
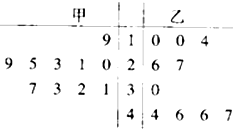 林业管理部门为了保证树苗的质量,在植物节前对所购进的树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗的高度,它们的高度用茎叶图表示如下(单位:厘米).若甲、乙两种树苗的平均高度分别是x甲,x乙,则下列结论正确的是( )
林业管理部门为了保证树苗的质量,在植物节前对所购进的树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗的高度,它们的高度用茎叶图表示如下(单位:厘米).若甲、乙两种树苗的平均高度分别是x甲,x乙,则下列结论正确的是( )| A、x甲>x乙,甲种树苗比乙种树苗高度更整齐 |
| B、x甲>x乙,乙种树苗比甲种树苗高度更整齐 |
| C、x甲<x乙,甲种树苗比乙种树苗高度更整齐 |
| D、x甲<x乙,乙种树苗比甲种树苗高度更整齐 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2m-x |
| 2+x |
| 1 |
| 2x |
查看答案和解析>>
科目:高中数学 来源: 题型:
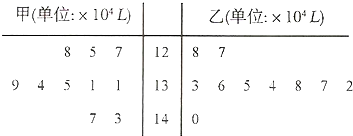
| A、133,133 |
| B、134,133 |
| C、134,134 |
| D、1343,134 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com