
| S | 2 △OAB |
| S | 2 △OAC |
| S | 2 △OBC |
| S | 2 △ABC |
| S | 2 △OAB |
| S | 2 △OAC |
| S | 2 △OBC |
| S | 2 △ABC |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| S | 2 △OAB |
| S | 2 △OAC |
| S | 2 △OBC |
| S | 2 △ABC |
| ||
| 2 |
| ||
| 2 |
| S | 2 △OAB |
| S | 2 △OAC |
| S | 2 △OBC |
| S | 2 △ABC |
| ||
| 2 |


 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
| ab | ||
|
| abc | ||
|
| abc | ||
|
查看答案和解析>>
科目:高中数学 来源:2014届海南琼海嘉积中学高二上教学监测(三)理科数学试卷(解析版) 题型:填空题
在平面几何里,已知直角△SAB的两边SA,SB互相垂直,且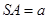 ,
,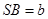 则
则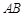 边上的高
边上的高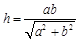 ; 拓展到空间,如图,三棱锥
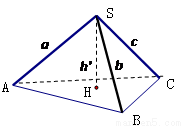
; 拓展到空间,如图,三棱锥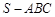 的三条侧棱SB、SB、SC两两相互垂直,且
的三条侧棱SB、SB、SC两两相互垂直,且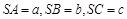 ,则点
,则点 到面
到面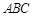 的距离
的距离
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁沈阳二中等重点中学协作体高三领航高考预测(十)文数学卷(解析版) 题型:填空题
在平面几何里,已知直角三角形ABC中,角C为
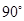 ,AC=b,BC=a,运用类比方法探求空间中三棱锥的有关结论:
,AC=b,BC=a,运用类比方法探求空间中三棱锥的有关结论:
有三角形的勾股定理,给出空间中三棱锥的有关结论:________
若三角形ABC的外接圆的半径为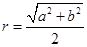 ,给出空间中三棱锥的有关结论:________
,给出空间中三棱锥的有关结论:________
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
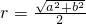 ,给出空间中三棱锥的有关结论:________.
,给出空间中三棱锥的有关结论:________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com