
【题目】已知隧道的截面是半径为4.0 m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7 m、高为3 m的货车能不能驶入这个隧道?假设货车的最大宽度为a m,那么要正常驶入该隧道,货车的限高为多少?
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:高中数学 来源: 题型:
【题目】性格色彩学创始人乐嘉是江苏电视台当红节目“非诚勿扰”的特约嘉宾,他的点评视角独特,语言犀利,给观众留下了深刻的印象,某报社为了了解观众对乐嘉的喜爱程度,随机调查了观看了该节目的140名观众,得到如下的列联表:(单位:名)
男 | 女 | 总计 | |
喜爱 | 40 | 60 | 100 |
不喜爱 | 20 | 20 | 40 |
总计 | 60 | 80 | 140 |
(Ⅰ)从这60名男观众中按对乐嘉是否喜爱采取分层抽样,抽取一个容量为6的样本,问样本中喜爱与不喜爱的观众各有多少名?
(Ⅱ)根据以上列联表,问能否在犯错误的概率不超过0.025%的前提下认为观众性别与喜爱乐嘉有关.(精确到0.001)
(Ⅲ)从(Ⅰ)中的6名男性观众中随机选取两名作跟踪调查,求选到的两名观众都喜爱乐嘉的概率.
附:
p(k2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k0 | 2.705 | 3.841 | 5.024 | 6.635 | 7.879 |
k2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的右焦点为F(1,0),点P是椭圆C上一动点,若动点P到点的距离的最大值为b2 .
的右焦点为F(1,0),点P是椭圆C上一动点,若动点P到点的距离的最大值为b2 .
(1)求椭圆C的方程,并写出其参数方程;
(2)求动点P到直线l:x+2y﹣9=0的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱锥P﹣ABC中,PA⊥平面ABC,△ABC为正三角形,PA=AB,E是PC的中点,则异面直线AE和PB所成角的余弦值为( ) 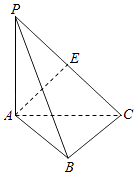
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD.

(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB.
查看答案和解析>>
科目:高中数学 来源: 题型:
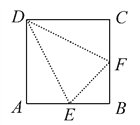
【题目】如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C重合,重合后记为点P.
问:(1)折起后形成的几何体是什么几何体?
(2)这个几何体共有几个面,每个面的三角形有何特点?
(3)每个面的三角形面积为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各对直线不互相垂直的是 ( )
A. l1的倾斜角为120°,l2过点P(1,0),Q(4, ![]() )
)
B. l1的斜率为-![]() ,l2过点P(1,1),Q
,l2过点P(1,1),Q![]()
C. l1的倾斜角为30°,l2过点P(3, ![]() ),Q(4,2
),Q(4,2![]() )
)
D. l1过点M(1,0),N(4,-5),l2过点P(-6,0),Q(-1,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com