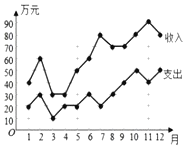
[题目]如图的折线图是某公司2018年1月至12月份的收入与支出数据.若从6月至11月这6个月中任意选2个月的数据进行分析.则这2个月的利润都不高于40万的概率为( )A.B.C.D. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】如图的折线图是某公司2018年1月至12月份的收入与支出数据，若从6月至11月这6个月中任意选2个月的数据进行分析，则这2个月的利润（利润＝收入﹣支出）都不高于40万的概率为（　　）

A.B.C.D.

【答案】B

【解析】

从7月至12月这6个月中任意选2个月的数据进行分析，基本事件总数，由折线图得6月至11月这6个月中利润（利润收入支出）低于40万的有6月，9月，10月，由此即可得到所求．

如图的折线图是某公司2017年1月至12月份的收入与支出数据，

从6月至11月这6个月中任意选2个月的数据进行分析，

基本事件总数，

由折线图得6月至11月这6个月中利润（利润收入支出）不高于40万的有6月，8月，9月，10月，

这2个月的利润（利润收入支出）都不高于40万包含的基本事件个数，

这2个月的利润（利润收入支出）都低于40万的概率为，

故选：

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数．

(I)求函数的对称轴方程；

(II)将函数的图象上各点的纵坐标保持不变，横坐标伸长为原来的2倍，然后再向左平移个单位，得到函数的图象．若分别是△ABC三个内角A，B，C的对边，a=2，c=4，且，求b的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在三棱锥中，，，，，分别是，的中点，在上且.

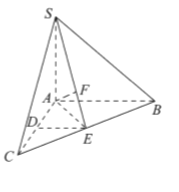
（I）求证：；

（II）求直线与平面所成角的正弦值；

（III）在线段上是否存在点，使二面角的大小为？若存在，求出的长；若不存在，请说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

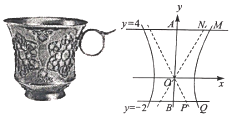
【题目】如图为陕西博物馆收藏的国宝——唐·金筐宝钿团花纹金杯,杯身曲线内收,玲珑娇美,巧夺天工,是唐代金银细作的典范之作.该杯型几何体的主体部分可近似看作是双曲线的右支与直线,,围成的曲边四边形绕轴旋转一周得到的几何体,如图分别为的渐近线与,的交点,曲边五边形绕轴旋转一周得到的几何体的体积可由祖恒原理(祖恒原理：幂势既同，则积不容异).意思是：两等高的几何体在同高处被截得的两截面面积均相等,那么这两个几何体的体积相等，那么这两个几何体的体积相等)，据此求得该金杯的容积是_____.(杯壁厚度忽略不计)