
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 处的切线平行于
处的切线平行于![]() 轴,求
轴,求![]() 的值和
的值和![]() 的极值;
的极值;
(2)若过点![]() 可作曲线
可作曲线![]() 的三条切线,求
的三条切线,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ,2,-2;(Ⅱ)
,2,-2;(Ⅱ)![]()
【解析】
试题(Ⅰ)求出原函数的导函数,由f(x)在x=1处的切线平行于x轴,可得f′(1)=0,由此求a的值,把a值代入导函数,求得导函数的零点,由导函数的零点对函数定义域分段,列表得到单调区间,则f(x)的极值可求;(Ⅱ)设出切点(t,t3+at),求导数,利用直线方程点斜式得到切线方程,代入A的坐标,化为关于t的方程,再利用导数求出关于t的函数的极值,由极大值大于0,且极小值小于0联立不等式组求得a的取值范围.
试题解析:(Ⅰ)![]() ,
,
∵![]() 在
在![]() 处的切线平行于
处的切线平行于![]() 轴, ∴
轴, ∴![]() ,即
,即![]() .
.
∴![]() .令
.令![]() ,得
,得![]() .
.
|
|
|
| 1 |
|
| + | 0 | - | 0 | + |
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
∴![]() ,
,![]() .
.
(Ⅱ)设切点为![]() ,则切线斜率为
,则切线斜率为![]() ,
,
∴切线方程为![]() , ∵点
, ∵点![]() 在切线上,
在切线上,
∴![]() , 即
, 即![]() . (*)
. (*)
于是, 若过点A可作曲线![]() 的三条切线, 则方程(*)有三个相异的实根根.
的三条切线, 则方程(*)有三个相异的实根根.
记![]() , 则
, 则![]() .
.
当![]() 时,
时,![]() ,
,![]() 是增函数,
是增函数,
当![]() 时,
时,![]() ,
,![]() 是减函数,
是减函数,
当![]() 时,
时,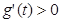 ,
,![]() 是增函数,
是增函数,
∴![]() .
.
要使方程(*)有三个相异实根, 则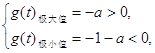 即
即![]() .
.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:高中数学 来源: 题型:
【题目】已知两个平面垂直,下列命题中错误的是( )
A.两个平面内分别垂直于交线的两条直线相互垂直
B.一个平面内的任一条直线必垂直于另一个平面.
C.一个平面内存在直线垂直于另一个平面
D.一个平面内的任意一条直线都垂直于另一个平面内的无数条直线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)如下图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E、F分别是BC、CC1的中点.
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F-AEC的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,x∈R.
,x∈R.
(1)判断函数的奇偶性,并说明理由;
(2)利用函数单调性定义证明:![]() 在
在![]() 上是增函数;
上是增函数;
(3)若![]() 对任意的x∈R,任意的
对任意的x∈R,任意的![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,M、N分别为棱BC和棱CC1的中点,则异面直线AC和MN所成的角为( )
A. 30° B. 45° C. 90° D. 60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数![]() 的图象,只要将函数
的图象,只要将函数![]() 的图象( )
的图象( )
A.每一点的横坐标变为原来的![]() 倍(纵坐标不变),再将所得图象向左平移
倍(纵坐标不变),再将所得图象向左平移![]() 个长度
个长度
B.每一点的横坐标变为原来的![]() 倍(纵坐标不变),再将所得图象向左平移
倍(纵坐标不变),再将所得图象向左平移![]() 个长度
个长度
C.向左平移![]() 个长度,再将所得图象每一点的横坐标变为原来的
个长度,再将所得图象每一点的横坐标变为原来的![]() 倍(纵坐标不变)
倍(纵坐标不变)
D.向左平移![]() 个长度,再将所得图象每一点的横坐标变为原来的
个长度,再将所得图象每一点的横坐标变为原来的![]() 倍(纵坐标不变)
倍(纵坐标不变)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若在定义域内存在实数![]() ,使得
,使得![]() 成立,则称函数有“和一点”
成立,则称函数有“和一点”![]() .
.
(1)函数![]() 是否有“和一点”?请说明理由;
是否有“和一点”?请说明理由;
(2)若函数![]() 有“和一点”,求实数
有“和一点”,求实数![]() 的取值范围;
的取值范围;
(3)求证:![]() 有“和一点”.
有“和一点”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com