
【题目】已知函数![]() .
.
(1)若![]() ,求出函数
,求出函数![]() 的单调区间及最大值;
的单调区间及最大值;
(2)若![]() 且
且![]() ,求函数
,求函数![]() 在
在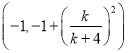 上的最大值
上的最大值![]() 的表达式.
的表达式.
【答案】(1)增区间为![]() ,减区间为
,减区间为![]() ;最大值为
;最大值为![]() ;(2)分类讨论,详见解析.
;(2)分类讨论,详见解析.
【解析】
(1)先求解导数,判断单调性,然后可得最值;
(2)先求解导数,分类讨论![]() 或
或![]() ,结合导数在区间上的符号,及根的大小关系,进行分类求解.
,结合导数在区间上的符号,及根的大小关系,进行分类求解.
(1)由已知,![]() 时,
时,![]() ,
,
故![]() ,
,
由![]() 得
得![]() ,所以
,所以![]() 的增区间为
的增区间为![]() 递增;
递增;
由![]() 得
得![]() ,所以
,所以![]() 的减区间为在
的减区间为在![]() ;
;
所以![]() .
.
(2)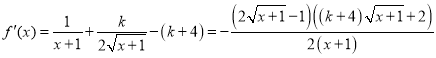 ,
,
![]()
![]() ,即
,即![]() 时,所以
时,所以![]() 在
在![]() 递增,在
递增,在![]() 递减,
递减,
下面比较![]() 与
与![]() 大小:
大小:
①当![]() ,即
,即![]() 或
或![]() 时,
时,
![]() ,
,
②当![]() ,即
,即![]() 或
或![]() 时,
时,
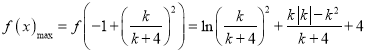 .
.
![]()
![]() ,即
,即![]() 时,由
时,由![]() 可得
可得![]() ,
,![]() ,
,
下面比较![]() ,
,![]() 大小:
大小:
①当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 递增,在
递增,在![]() 递减,在
递减,在![]() 递增,
递增,
又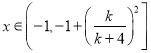 ,故
,故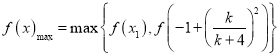 ,
,
由![]() 知
知![]() ,
,
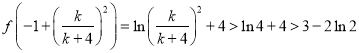
![]() ,
,
故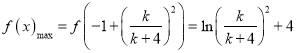 ;
;
②当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 递增,在
递增,在![]() 递减,在
递减,在![]() 递增,
递增,
则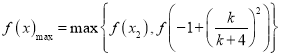
 ,
,
而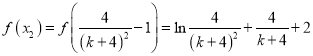
![]() (利用重要不等式
(利用重要不等式![]() )
)
又![]() ,知
,知![]() ,故
,故 ,
,
所以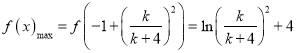 ;
;
③当![]() ,即
,即![]() 时,
时,![]() ,即
,即![]() 在
在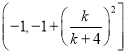 单调递增,
单调递增,
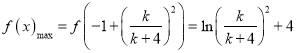 ;
;
综上所述,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,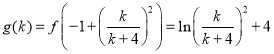 ;
;
当![]() 时,
时,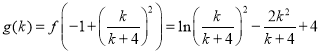 .
.


科目:高中数学 来源: 题型:
【题目】某市据实际情况主要采取以下四种扶贫方式:第一,以工代赈方式,指政府投资建设基础设施工程,组织贫困地区群众参加工程建设并获得劳务报酬,第二,整村推进方式指以贫困村为具体帮扶对象,帮扶对口到村,资金安排到村,扶贫效益到户,第三,科技扶贫方式,指组织科技人员深入贫困乡村实地指导、技术培训等传授科技知识,第四,移民搬迁方式,指对目前极少数居住在生存条件恶劣、自然资源贫乏地区的特困人口,实行自愿移民,该市为了2020年更好的完成精准扶贫各项任务,2020年初在全市贫困户(分一般贫困户和“五特”户两类)中随机抽取了5000户就目前的主要四种扶贫方式行了问卷调查,支持每种扶贫方式的结果如表:
调查的贫困户 | 支持以工代赈户数 | 支持整村推进户数 | 支持科技扶贫户数 | 支持移民搬迁户数 |
一般贫困户 | 1200 | 1600 |
| 200 |
五特户(五保户和特困户) | 100 |
|
| 100 |
已知在被调查的5000户中随机抽取一户支持整村推进的概率为0.36.
(Ⅰ)现用分层抽样的方法在所有参与调查的贫困户中抽取50户进行深入访谈,问应在支持科技扶贫户数中抽取多少户?
(Ⅱ)虽然“五特”户在全市的贫困户所占比例不大,但本次调查要有意义,其中这次调查的“五特”户户数不能低于被调查总户数的9.2%,已知![]() ,求本次调查有意义的概率是多少?
,求本次调查有意义的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体![]() 中,
中,![]() 是棱
是棱![]() 的中点,
的中点,![]() 是侧面
是侧面![]() 上的动点,且
上的动点,且![]() 平面
平面![]() ,记
,记![]() 与
与![]() 的轨迹构成的平面为
的轨迹构成的平面为![]() .
.
①![]() ,使得
,使得![]() ;
;
②直线![]() 与直线
与直线![]() 所成角的正切值的取值范围是
所成角的正切值的取值范围是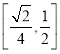 ;
;
③![]() 与平面
与平面![]() 所成锐二面角的正切值为
所成锐二面角的正切值为![]() ;
;
④正方体![]() 的各个侧面中,与
的各个侧面中,与![]() 所成的锐二面角相等的侧面共四个.
所成的锐二面角相等的侧面共四个.
其中正确命题的序号是________.(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 交曲线
交曲线![]() 于
于![]() 两点,
两点,![]() 为
为![]() 中点.
中点.
(1)求曲线![]() 的直角坐标方程和点
的直角坐标方程和点![]() 的轨迹
的轨迹![]() 的极坐标方程;
的极坐标方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列![]() 中,已知
中,已知![]() ,
,![]() .设数列
.设数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() ,
,![]() (
(![]() ,
,![]() ).
).
(1)求数列![]() 的通项公式;
的通项公式;
(2)证明:数列![]() 是等差数列;
是等差数列;
(3)是否存在等差数列![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ?若存在,求出所有符合题意的等差数列
?若存在,求出所有符合题意的等差数列![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从抛物线C:![]() (
(![]() )外一点作该抛物线的两条切线PA、PB(切点分别为A、B),分别与x轴相交于C、D,若AB与y轴相交于点Q,点
)外一点作该抛物线的两条切线PA、PB(切点分别为A、B),分别与x轴相交于C、D,若AB与y轴相交于点Q,点![]() 在抛物线C上,且
在抛物线C上,且![]() (F为抛物线的焦点).
(F为抛物线的焦点).
(1)求抛物线C的方程;
(2)①求证:四边形![]() 是平行四边形.
是平行四边形.
②四边形![]() 能否为矩形?若能,求出点Q的坐标;若不能,请说明理由.
能否为矩形?若能,求出点Q的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com