练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】(多选题)下列说法中正确的是（ ）

    A.在频率分布直方图中，中位数左边和右边的直方图的面积相等.

    B.若A、B为互斥事件，则A的对立事件与B的对立事件一定互斥.

    C.某个班级内有40名学生，抽10名同学去参加某项活动，则每4人中必有1人抽中.

    D.若回归直线的斜率，则变量与正相关.

    【答案】AD

    【解析】

    利用频率分布直方图和回归直线方程，以及互斥事件和对立事件的概念，逐项判定，即可求解．

    对于A中，在频率分布直方图中，根据中位数的概念，可得中位数左边和右边的直方图的面积相等是正确的；

    对于B中，若A、B为互斥事件，根据互斥事件和对立事件的概念，可得则A的对立事件与B的对立事件不一定互斥，所以不正确；

    对于C中，某个班级内有40名学生，抽10名同学去参加某项活动，根据概率的概念，可得每4人中不一定必有1人抽中，所以是不正确的；

    对于D中，若回归直线的斜率，根据回归系数的含义，可得变量与正相关是正确的．

    故选：AD．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知圆：与直线：，动直线过定点.

    （1）若直线与圆相切，求直线的方程；

    （2）若直线与圆相交于、两点，点M是PQ的中点，直线与直线相交于点N．探索是否为定值，若是，求出该定值；若不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个孩子的身高与年龄（周岁）具有相关关系，根据所采集的数据得到线性回归方程，则下列说法错误的是（ ）

    A.回归直线一定经过样本点中心

    B.斜率的估计值等于6.217，说明年龄每增加一个单位，身高就约增加6.217个单位

    C.年龄为10时，求得身高是，所以这名孩子的身高一定是

    D.身高与年龄成正相关关系

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）当时，求曲线在点处的切线方程；

    （Ⅱ）当时，证明： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（ ）

    A. 1盏 B. 3盏 C. 5盏 D. 9盏

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,设点为椭圆的右焦点，圆过且斜率为的直线交圆于两点，交椭圆于点两点，已知当时，

    （1）求椭圆的方程.

    （2）当时，求的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费（单位：万元）对年销售量（单位：）的影响，对近年的年宣传费和年销售量作了初步统计和处理，得到的数据如下：

    年宣传费（单位：万元）

    年销售量（单位：）

    ，.

    （1）在给定的坐标系中画出表中数据的散点图；

    （2）求出关于的线性回归方程；

    （3）若公司计划下一年度投入宣传费万元，试预测年销售量的值.

    参考公式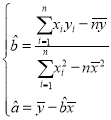

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线的右顶点到其一条渐近线的距离等于，抛物线的焦点与双曲线的右焦点重合，则抛物线上的动点到直线和的距离之和的最小值为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】《数书九章》是中国南宋时期杰出数学家秦九韶的著作，其中在卷五“三斜求积”中提出了已知三角形三边、、，求面积的公式，这与古希腊的海伦公式完全等价，其求法是“以小斜冥并大斜冥减中斜冥，余半之，自乘于上，以小斜冥乘大斜冥减上，余四约之，为实．一为从隅，开平方得积”若把以上这段文字写出公式，即若，则．

    （1）已知的三边，，，且，求证：的面积．

    （2）若，，求的面积的最大值．

    查看答案和解析>>

    同步练习册答案