
 ,
, ,
, ,有下列三个命题:
,有下列三个命题: •
• =
= •
• ,则
,则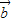 =
= 、
、 =(1,k),
=(1,k), =(-2,6),
=(-2,6), ∥
∥ ,则k=-3.
,则k=-3. 和
和 满足|
满足| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 +
+ 的夹角为60°.
的夹角为60°.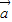 ,
,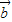 ,
,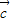 的关系;
的关系;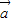 ∥
∥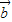 ,我们根据两个向量平行,坐标交叉相乘差为0的原则,可以构造一个关于k的方程,解方程即可求出k值;
,我们根据两个向量平行,坐标交叉相乘差为0的原则,可以构造一个关于k的方程,解方程即可求出k值;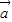 |=|
|=|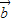 |=|
|=|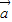 -
-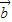 |,我们利用向量加减法的平行四边形法则,可以画出满足条件图象,利用图象易得到两个向量的夹角;
|,我们利用向量加减法的平行四边形法则,可以画出满足条件图象,利用图象易得到两个向量的夹角; 解:①若
解:①若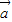 •
•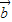 =
=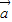 •
•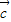 ,则
,则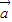 •(
•(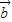 -
-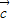 )=0,此时
)=0,此时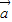 ⊥(
⊥(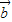 -
-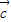 ),而不一定
),而不一定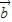 =
=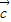 ,①为假.
,①为假.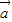 ∥
∥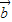 的充要条件,知1×6-k•(-2)=0,解得k=-3,②为真.
的充要条件,知1×6-k•(-2)=0,解得k=-3,②为真.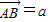 ,
,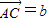 ,
,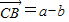 ,
, |=|
|=|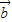 |=|
|=|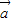 -
- |,可知△ABC为等边三角形.
|,可知△ABC为等边三角形.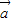 +
+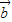 =
=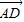 ,
,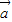 与
与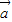 +
+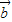 成的角为30°.③为假.
成的角为30°.③为假.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源:2012-2013学年安徽省马鞍山市高一(上)期末数学试卷(解析版) 题型:填空题
 ,
, ,
, ,有下列几个命题:
,有下列几个命题: ,则
,则 或
或 ;
; 与
与 均为单位向量,它们的夹角为60°,则
均为单位向量,它们的夹角为60°,则 ;
; ,
, ,
, 满足
满足 ,
, ,则
,则 与
与 的夹角为120°;
的夹角为120°; ,
, ,则
,则 在
在 方向上的投影是-1.
方向上的投影是-1.查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省外语外贸大学附设外语学校高三(上)数学寒假作业3(文科)(解析版) 题型:选择题
 ,
, ,
, .有下列三个命题:
.有下列三个命题: •
• =
= •
• ,则
,则 =
= .
. =(1,k),
=(1,k), =(-2,6),
=(-2,6), ∥
∥ ,则k=-3.
,则k=-3. 和
和 满足|
满足| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 +
+ 的夹角为60°.
的夹角为60°.查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省潍坊市现代中学高三(上)12月月考数学试卷(文科)(解析版) 题型:填空题
 ,
, ,
, ,有下列三个命题:
,有下列三个命题: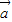 •
• =
= •
• ,则
,则 =
= 、
、 =(1,k),
=(1,k), =(-2,6),
=(-2,6), ∥
∥ ,则k=-3.
,则k=-3. 和
和 满足|
满足| |=|
|=| |=|
|=|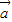 -
- |,则
|,则 与
与 +
+ 的夹角为60°.
的夹角为60°.查看答案和解析>>
科目:高中数学 来源:2008年陕西省高考数学试卷(文科)(解析版) 题型:解答题
 ,
, ,
, ,有下列三个命题:
,有下列三个命题: •
• =
= •
• ,则
,则 =
= 、
、 =(1,k),
=(1,k),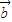 =(-2,6),
=(-2,6), ∥
∥ ,则k=-3.
,则k=-3. 和
和 满足|
满足| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 +
+ 的夹角为60°.
的夹角为60°.查看答案和解析>>
科目:高中数学 来源:2008年陕西省高考数学试卷(理科)(解析版) 题型:解答题
 ,
, ,
, ,有下列三个命题:
,有下列三个命题: •
• =
= •
• ,则
,则 =
= 、
、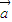 =(1,k),
=(1,k), =(-2,6),
=(-2,6), ∥
∥ ,则k=-3.
,则k=-3. 和
和 满足|
满足| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 +
+ 的夹角为60°.
的夹角为60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com