已知a、b都为正数且满足a+b+ab=3,则a+b的最小值为 .
【答案】
分析:本题从形式上看可以利用基本不等式把所给的等式转化为关于a+b不等式,解出其范围,即可得到所求的最小值.
解答:解:∵a、b都为正数且满足a+b+ab=3,
∴a+b+
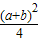
≥3等号当a=b时成立.
∴(a+b)
2+4(a+b)-12≥0
∴a+b≥2或a+b≤-6(舍)
a+b的最小值为2
故答案为2
点评:本题考查基本不等式,求解本题的关键是利用基本不等式的特点将方程变为不等式,从而解不等式得出所求的范围,由于基本不等式有几种形式,故解题时要根据题设中的条件选择恰当的形式进行变换.
