练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在极坐标系中，圆C的方程为ρ=2acosθ（a≠0），以极点为坐标原点，极轴为x轴正半轴建立平面直角坐标系，设直线l的参数方程为 （t为参数）．
    （1）求圆C的标准方程和直线l的普通方程；
    （2）若直线l与圆C恒有公共点，求实数a的取值范围．

    【答案】
    （1）解：由 得， ，则 ，

    ∴直线l的普通方程为：4x﹣3y+5=0，

    由ρ=2acosθ得，ρ2=2aρcosθ

    又∵ρ2=x2+y2，ρcosθ=x

    ∴圆C的标准方程为（x﹣a）2+y2=a2，


    （2）解：∵直线l与圆C恒有公共点，∴ ，

    两边平方得9a2﹣40a﹣25≥0，∴（9a+5）（a﹣5）≥0

    ∴a的取值范围是 ．


    【解析】（1）根据ρ2=x2+y2 ， x=ρcosθ，y=ρsinθ把圆C的极坐标方程，由消元法把直线l的参数方程化为普通方程；（2）根据直线l与圆C有公共点的几何条件，建立关于a的不等式关系，解之即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】参加衡水中学数学选修课的同学，对某公司的一种产品销量与价格进行统计，得到如下数据和散点图：

    定价（元/）

    年销售

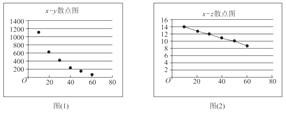
    （参考数据：

    ）

    （I）根据散点图判断，与，与哪一对具有较强的线性相关性（给出判断即可，不必说明理由）？

    （II）根据（I）的判断结果有数据，建立关于的回归方程（方程中的系数均保留两位有效数字）；

    （III）定价为多少元/时，年利润的预报值最大？

    附：对一组数据，其回归直线的斜率和截距的最小二乘估计分别为：.

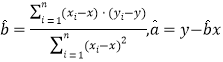    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的方程为，过点的一条直线与抛物线交于两点，若抛物线在两点的切线交于点.

    （1）求点的轨迹方程；

    （2）设直线与直线的夹角为，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在R上的奇函数f（x），当x≥0时，f（x）=x2﹣3x．则关于x的方程f（x）=x+3的解集为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线 x+y﹣ =0经过椭圆C： + =1（a＞b＞0）的右焦点和上顶点．
    （1）求椭圆C的标准方程；
    （2）过点（0，﹣2）的直线l与椭圆C交于不同的A，B两点，若∠AOB为钝角，求直线l的斜率k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【2017安徽阜阳二模】一企业从某生产线上随机抽取件产品，测量这些产品的某项技术指标值，得到的频率分布直方图如图.

    （1）估计该技术指标值平均数；

    （2）在直方图的技术指标值分组中，以落入各区间的频率作为取该区间值的频率，若，则产品不合格，现该企业每天从该生产线上随机抽取件产品检测，记不合格产品的个数为，求的数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{an}满足：a4=7，a10=19，其前n项和为Sn ．
    （1）求数列{an}的通项公式an及Sn；
    （2）若等比数列{bn}的前n项和为Tn ， 且b1=2，b4=S4 ， 求Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，已知点A（2，4），直线l：x﹣2y+1=0．
    （1）求过点A且平行于l的直线的方程；
    （2）若点M在直线l上，且AM⊥l，求点M的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】袋中有外形、质量完全相同的红球、黑球、黄球、绿球共12个．从中任取一球，得到红球的概率是 ，得到黑球或黄球的概率是 ，得到黄球或绿球的概率也是 ．
    （1）试分别求得到黑球、黄球、绿球的概率；
    （2）从中任取一球，求得到的不是“红球或绿球”的概率．

    查看答案和解析>>

    同步练习册答案