
����Ŀ��ij������Ϸ�����ǣ��Ⱥ�����ö���ӣ����������ظ�n�֣���n�ֵĵ����ֱ��Ϊxn �� yn �� �����������xn�� ![]() ������Ϊ��n�ִ��سɹ������������һ��Ͷ����ֱ�����سɹ�����Ϸ������
������Ϊ��n�ִ��سɹ������������һ��Ͷ����ֱ�����سɹ�����Ϸ������
�������һ�ִ��سɹ��ĸ��ʣ�
���������i�ִ��سɹ�����Ľ�����f��i��=10000�� ![]() ����λ��Ԫ������ij�˴��ػ�ý�����1250Ԫ�ĸ��ʣ�
����λ��Ԫ������ij�˴��ػ�ý�����1250Ԫ�ĸ��ʣ�
���������Ϸֻ���е������֣������ֺ�����Ϸ�ɹ������ֹ��Ϸ���ǽ��е�����Ϊ�������X����x�ķֲ��к���ѧ������
���𰸡��⣺������y1=6ʱ��y1�� ![]() �����x1=1��2�� ��y1=5ʱ��y1��
�����x1=1��2�� ��y1=5ʱ��y1�� ![]() �����x1=1��2��
�����x1=1��2��
��y1=4ʱ��y1�� ![]() �����x1=1��2��
�����x1=1��2��
��y1=3ʱ��y1�� ![]() �����x1=1��
�����x1=1��
��y1=2ʱ��y1�� ![]() ���x1=1��
���x1=1��
��y1=1ʱ��y1�� ![]() �����x1��ֵ��
�����x1��ֵ��
���һ�ִ��سɹ��ĸ���P��A��= ![]() ��
��
���������f��i��=10000�� ![]() ��1250����i��3��
��1250����i��3��
�ɣ���ÿ�ֹ��صĸ���Ϊ ![]() ��
��
ij�˴��ػ�ý�����1250Ԫ�ĸ���
��P��i��3��=1��P��i=1����P��i=2��=1�� ![]() ����1��
����1�� ![]() ����
���� ![]() =
= ![]()
����������X�Ŀ���ȡֵΪ1��2��3��4
����Ϸ��k�ֺ���ֹ�ĸ���Ϊpk��k=1��2��3��4��
p1= ![]() ��p2=��1��
��p2=��1�� ![]() ����
���� ![]() =
= ![]() ��p3=��1��
��p3=��1�� ![]() ��2��
��2�� ![]() =
= ![]() ��p4=1��p2��p3=
��p4=1��p2��p3= ![]() ��
��
��X�ķֲ���Ϊ
X | 1 | 2 | 3 | 4 |
P |
|
|
|
|
���EX=1�� ![]() +2��
+2�� ![]() +3��
+3�� ![]() +4��
+4�� ![]() =
= ![]()
������������ö�ٷ��г������������������ԣ�x1 �� y1�����ɣ�������10000�� ![]() ��1250����i��3���ɣ���ÿ�ֹ��صĸ���Ϊ
��1250����i��3���ɣ���ÿ�ֹ��صĸ���Ϊ ![]() ��ij�˴��ػ�ý�����1250Ԫ�ĸ��ʣ�P��i��3��=1��P��i=1����P��i=2����������Ϸ��k�ֺ���ֹ�ĸ���Ϊpk��k=1��2��3��4�����ֱ������Ӧ�ĸ��ʣ��������X�ķֲ��к���ѧ������
��ij�˴��ػ�ý�����1250Ԫ�ĸ��ʣ�P��i��3��=1��P��i=1����P��i=2����������Ϸ��k�ֺ���ֹ�ĸ���Ϊpk��k=1��2��3��4�����ֱ������Ӧ�ĸ��ʣ��������X�ķֲ��к���ѧ������


 �ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��l�IJ�������Ϊ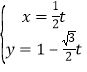 (tΪ����
(tΪ����![]() ������ԭ��Ϊ���㣬x��������Ϊ���Ὠ��������ϵ��ԲC�ļ����귽��Ϊ
������ԭ��Ϊ���㣬x��������Ϊ���Ὠ��������ϵ��ԲC�ļ����귽��Ϊ![]() ��
��
![]() ��
��![]() �ж�ֱ��l��ԲC�Ľ��������
�ж�ֱ��l��ԲC�Ľ��������
![]() ��
��![]() ��ԲC��ֱ��l����A��B���㣬���߶�AB�ij��ȣ�
��ԲC��ֱ��l����A��B���㣬���߶�AB�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ������ˮƽ�����ϵ����壬�ܵ������ˮƽ����F�����ã�F�Ĵ�С��ʱ��t�Ĺ�ϵ�������˶��ٶ�v��ʱ��t�Ĺ�ϵ��ͼ����ʾ�������ж���ȷ���ǣ�
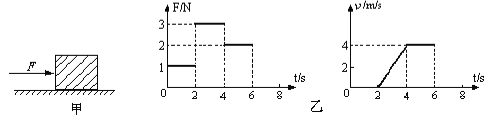
A.t��3sʱ�������ܵ����ĺ���Ϊ��
B.t��6sʱ����F�������������̾�ֹ
C.2s��4s����������Ħ����������
D.t��1sʱ����������Ħ������1N
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ���ɷ�֤����![]() �ܱ�3�������ĵڶ����У�
�ܱ�3�������ĵڶ����У�![]() ʱ��Ϊ��ʹ�ü��裬Ӧ��5k��1��2k��1����Ϊ(��)��
ʱ��Ϊ��ʹ�ü��裬Ӧ��5k��1��2k��1����Ϊ(��)��
A. (5k��2k)��4��5k��2k B. 5(5k��2k)��3��2k
C. (5��2)(5k��2k) D. 2(5k��2k)��3��5k
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ˮ��ɽ���ǽ�ɽ��ɽ����Ϊ�˱������������ٿ�����Ⱦ��ij�������������쳧������Ͷ������ij�ֻ����͵Ŀ����������������������������۾���õ����������۵�ͳ�ƹ������£�����̶������ɱ�Ϊ2��Ԫ����ÿ�������ͺſ���������1��̨���ɱ�����1��Ԫ����������x��̨���������� ����Ԫ�����ٶ������ĸ��ͺſ������������������������������멁�����ɱ�����
����Ԫ�����ٶ������ĸ��ͺſ������������������������������멁�����ɱ�����
��1��Ϊʹ�ò�Ʒ�������������������xӦ������ʲô��Χ�ڣ�
��2���ò�Ʒ��������̨ʱ����ʹ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ��ֱ������ϵ�У���ԲC�IJ�������Ϊ ![]() ����Ϊ��������
������������
��1����ԭ��Ϊ���㣬x���������Ϊ���Ὠ��������ϵ������ԲC�ļ����귽�̣�
��2����M��x��y��Ϊ��ԲC������һ�㣬��x+2y��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ʒ��![]() ����ÿ�������ۼ۸�
����ÿ�������ۼ۸�![]() ��Ԫ����ʱ��
��Ԫ����ʱ��![]() ��
��![]() �����죩�ĺ�����ϵ���㺯��
�����죩�ĺ�����ϵ���㺯��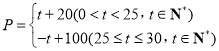 ������Ʒ��
������Ʒ��![]() ������������
������������![]() ��������ʱ��
��������ʱ��![]() ��
��![]() �����죩֮������һ�κ�����ϵ���±���
�����죩֮������һ�κ�����ϵ���±���
�� |
|
|
|
|
|
|
|
|
|
��1�����ݱ����ṩ�����ݣ�ȷ����������![]() ��ʱ��
��ʱ��![]() ��һ�κ�����ϵʽ��
��һ�κ�����ϵʽ��
��2�������Ʒ�������۽������ֵ��ָ�������۽������һ����![]() ���еĵڼ���,�������۽��
���еĵڼ���,�������۽��![]() ÿ�������ۼ۸�
ÿ�������ۼ۸�![]() ����������
����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ݴ���ʱʹ�õ��Ƕ����ƣ�����ʮ���Ƶ�1��2��3��4�ڶ����Ʒֱ��ʾΪ1��10��11��100��������ijͬѧ��ƵĽ���������11111��Ϊʮ��������һ������ͼ�����жϿ���Ӧ����������ǣ� �� 
A.i��4
B.i��4
C.i��5
D.i��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����{an}���ȱ�����{bn}���㣺a1��b1��1��a2��b2��2a3��b3��1.
(1)������{an}��{bn}��ͨ�ʽ��
(2)��cn��anbn��������{cn}��ǰn���Sn.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com