
【题目】在四棱柱![]() 中,底面
中,底面![]() 为矩形,面
为矩形,面![]() ⊥平面
⊥平面![]() ,
,![]() =
=![]() =
=![]() =
=![]() ,
,![]() =2,
=2,![]() 是
是![]() 的中点.
的中点.
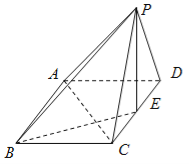
(Ⅰ)求证:![]() ⊥
⊥![]() ;
;
(Ⅱ)求BD与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】(Ⅰ)∵PD=PC,E为CD的中点,∴PE⊥CD,
∵平面PCD⊥平面ABCD,∴PE⊥平面ABCD,
∴PE⊥AC,(2分)
在Rt△BCE和Rt△ABC中,![]() ,∠ABC=∠BCE=90°,
,∠ABC=∠BCE=90°,
∴Rt△BCE∽Rt△ABC,(4分)
∴∠BAC=∠CBE,∠ACB=∠BEC,
∴∠EBC+∠ACB=∠CAB+∠ACB=90°,
∴BE⊥CA,(5分)
∵BE∩PE=E,
∴AC⊥平面PBE,
∴AC⊥PB;(6分)
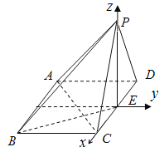
(Ⅱ)以E为坐标原点,如图建立空间直角坐标系,则P(0,0,1),C(1,0,0),![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,(8分)
,(8分)
设平面![]() 的法向量为
的法向量为![]() ,则
,则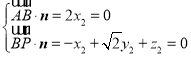 ,取
,取![]() =
=![]() ,则
,则![]() =0,
=0,![]() =-2,∴
=-2,∴![]() =(0,
=(0,![]() ,-2),(10分)
,-2),(10分)
设BD与平面![]() 所成角为
所成角为![]() ,
,
则![]() =
=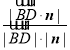 =
=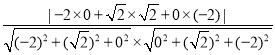 =
=![]() ,(11分)
,(11分)
∴BD与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .(12分)
.(12分)


科目:高中数学 来源: 题型:
【题目】现阶段全国多地空气质量指数“爆表”.为探究车流量与![]() 浓度是否相关,现对北方某中心城市的车流量最大的地区进行检测,现采集到
浓度是否相关,现对北方某中心城市的车流量最大的地区进行检测,现采集到![]() 月某天
月某天![]() 个不同时段车流量与
个不同时段车流量与![]() 浓度的数据,如下表:
浓度的数据,如下表:
车流量 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据上表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)规定当![]() 浓度平均值在
浓度平均值在![]() ,空气质量等级为优;当
,空气质量等级为优;当![]() 浓度平均值在
浓度平均值在![]() ,空气质量等级为良;为使该城市空气质量为优和良,利用该回归方程,预测要将车流量控制在每小时多少万辆内(结果以万辆做单位,保留整数).
,空气质量等级为良;为使该城市空气质量为优和良,利用该回归方程,预测要将车流量控制在每小时多少万辆内(结果以万辆做单位,保留整数).
附:回归直线方程: ![]() ,其中
,其中 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰好有一个元素,求
的解集中恰好有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足a1=1,nan+1=(n+1)an+n(n+1),n∈N* . (Ⅰ)证明:数列{ ![]() }是等差数列;
}是等差数列;
(Ⅱ)设bn=3n ![]() ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学调查了某班全部50名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 6 |
未参加演讲社团 | 6 | 30 |
(I)从该班随机选1名同学,求该同学至少参加上述一个社团的概率;
(II)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学A1,A2,A3,A4,A5,3名女同学B1,B2,B3,现从这5名男同学和3名女同学中各随机选1人,求A1被选中且B1未被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后随机投掷2枚正方体骰子,其中x表示第1枚骰子出现的点数,y表示第2枚骰子出现的点数,
(1)求点P(x,y)在直线y=x﹣1上的概率;
(2)求点P(x,y)满足y2<4x的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() . 问:是否存在正数m,使得对于任意正数
. 问:是否存在正数m,使得对于任意正数![]() ,可使
,可使![]() 为三角形的三边构成三角形?如果存在:①试写出一组x,y,m的值,②求出所有m的值;如果不存在,请说明理由.
为三角形的三边构成三角形?如果存在:①试写出一组x,y,m的值,②求出所有m的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产业结构,调整出x(x∈N*)名员工从事第三产业,调整后他们平均每人每年创造利润为10(a﹣ ![]() )万元(a>0),剩下的员工平均每人每年创造的利润为原来(1+
)万元(a>0),剩下的员工平均每人每年创造的利润为原来(1+ ![]() )倍.
)倍.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多可以整出多少名员工从事第三产业;
(2)若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润,则a的最大取值是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com