
【题目】已知数列{an}的前n项和为Sn , 且Sn=n2+2n;数列{bn}是公比大于1的等比数列,且满足b1+b4=9,b2b3=8.
(Ⅰ)分别求数列{an},{bn}的通项公式;
(Ⅱ)若cn=(﹣1)nSn+anbn , 求数列{cn}的前n项和Tn .
【答案】解:(I)∵Sn=n2+2n,∴当n=1时,a1=S1=3;
当n≥2时,an=Sn﹣Sn﹣1=n2+2n﹣[(n﹣1)2+2(n﹣1)]=2n+1.当n=1时也成立,∴an=2n+1.
设等比数列{bn}的公比q>1,∵b1+b4=9,b2b3=8.
∴ ![]() =9,
=9, ![]() q3=8,q>1.
q3=8,q>1.
联立解得b1=1,q=2.
∴bn=2n﹣1 .
(II)cn=(﹣1)nSn+anbn=(﹣1)n(n2+2n)+(2n+1)2n﹣1 .
设数列{(﹣1)nSn},{anbn}的前n项和分别为:An , Bn .
∵(﹣1)2k﹣1S2k﹣1+(﹣1)2kS2k=[(2k)2+22k]﹣[(2k﹣1)2+2(2k﹣1)]=4k+1,
则An=A2k=4×(1+2+…+k)+k=4× ![]() +k=k(2k+3)=
+k=k(2k+3)= ![]() ;
;
An=A2k﹣1=An+1﹣[(n+1)2+2(n+1)]= ![]() ﹣[(n+1)2﹣2(n+1)]=﹣
﹣[(n+1)2﹣2(n+1)]=﹣ ![]() .
.
Bn=3×1+5×2+7×22+…+(2n+1)2n﹣1 ,
2Bn=3×2+5×22+…+(2n﹣1)2n﹣2+(2n+1)2n ,
∴﹣Bn=3+2(2+22+…+2n﹣1)﹣(2n+1)2n= ![]() +1﹣(2n+1)2n=(1﹣2n)2n﹣1,
+1﹣(2n+1)2n=(1﹣2n)2n﹣1,
∴Bn=(2n﹣1)2n+1.
∴数列{cn}的前n项和Tn= 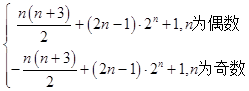
【解析】(I)由Sn=n2+2n,可得当n=1时,a1=S1=3;当n≥2时,an=Sn﹣Sn﹣1 . 即可得出an .
设等比数列{bn}的公比q>1,由b1+b4=9,b2b3=8.可得 ![]() =9,
=9, ![]() q3=8,q>1.联立解得即可得出.(II)cn=(﹣1)nSn+anbn=(﹣1)n(n2+2n)+(2n+1)2n﹣1 . 设数列{(﹣1)nSn},{anbn}的前n项和分别为:An , Bn . 利用“分组求和”与“错位相减法”、等比数列的前n项和公式即可得出.
q3=8,q>1.联立解得即可得出.(II)cn=(﹣1)nSn+anbn=(﹣1)n(n2+2n)+(2n+1)2n﹣1 . 设数列{(﹣1)nSn},{anbn}的前n项和分别为:An , Bn . 利用“分组求和”与“错位相减法”、等比数列的前n项和公式即可得出.
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系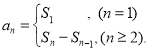 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】已知△ABC内角A,B,C的对边分别是a,b,c,且满足a( ![]() sinC+cosC)=b+c.
sinC+cosC)=b+c.
(I) 求角A的大小;
(Ⅱ)已知函数f(x)=sin(ωx+A)的最小正周期为π,求f(x)的减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化肥厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料.生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示:
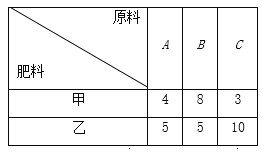
现有A种原料200吨,B种原料360吨,C种原料300吨.在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.分别用x,y表示计划生产甲、乙两种肥料的车皮数.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?并求出此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分15分)如图,在四棱锥![]() 中,平面PAD⊥平面ABCD,
中,平面PAD⊥平面ABCD, ![]() ,
,![]() ,E是BD的中点.
,E是BD的中点.

(Ⅰ)求证:EC//平面APD;
(Ⅱ)求BP与平面ABCD所成角的正切值;
(Ⅲ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的中位数是83,乙班学生成绩的平均数是86,则x+y的值为( ) 
A.168
B.169
C.8
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)是定义在(0,+∞)上单调函数,且对x∈(0,+∞),都有f(f(x)﹣lnx)=e+1,则方程f(x)﹣f′(x)=e的实数解所在的区间是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.(1,e)
D.(e,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
![]()
为了研究计算的方便,工作人员将上表的数据进行了处理,![]() 得到下表2:
得到下表2:
![]()
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)通过(1)中的方程,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)用所求回归方程预测到2010年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中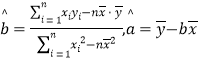 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com