
 某中学高三年级有400名学生参加月考,用简单随机抽样的方法抽取了一个容量为50的样本,得到数学成绩的频率分布直方图如图所示.
某中学高三年级有400名学生参加月考,用简单随机抽样的方法抽取了一个容量为50的样本,得到数学成绩的频率分布直方图如图所示.分析 (Ⅰ)由频率分布直方图,能求出第四个矩形的高.
(Ⅱ)求出成绩不低于120分的频率,由此可估计高三年级不低于120分的人数.
(Ⅲ)由直方图知,成绩在[140,150]的人数是6人,其中女生为A,B,男生为c,d,e,f,利用列举法能求出这6人中抽取2人,其中男生女生各一名的概率.
解答 (本小题满分12分)
解:(Ⅰ)由频率分布直方图,
第四个矩形的高是[1-(0.010+0.012+0.020+0.030)×10]÷10=0.028.…(4分)
(Ⅱ)成绩不低于1(20分)的频率是1-(0.010+0.020)×10=0.7,
可估计高三年级不低于1(20分)的人数为400×0.7=280人.…(7分)
(Ⅲ)由直方图知,成绩在[140,150]的人数是0.012×10×50=6,
记女生为A,B,男生为c,d,e,f,这6人中抽取2人的情况有
AB,Ac,Ad,Ae,Af,Bc,Bd,Be,Bf,cd,ce,cf,de,df,ef,共15种.…(9分)
其中男生女生各一名的有8种,概率为=$\frac{8}{15}$.…(12分)
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
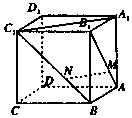 正方体ABCD-A1B1C1D1中,点M、N分别在线段AB1、BC1上,且AM=BN.以下结论:①AA1⊥MN;②A1C1∥MN;③MN∥平面A1B1C1D1;④MN与A1C1异面,⑤MN与 A1C1成30°.其中有可能成立的结论的个数为( )
正方体ABCD-A1B1C1D1中,点M、N分别在线段AB1、BC1上,且AM=BN.以下结论:①AA1⊥MN;②A1C1∥MN;③MN∥平面A1B1C1D1;④MN与A1C1异面,⑤MN与 A1C1成30°.其中有可能成立的结论的个数为( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,-\frac{5}{2}]$ | B. | $(-\frac{5}{2},-\frac{3}{2}]$ | C. | $[-\frac{5}{2},-\frac{3}{2}]$ | D. | $(-\frac{3}{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | -8 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
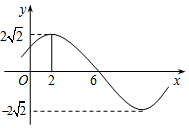
| A. | $ω=\frac{π}{8}{,_{\;}}φ=\frac{3π}{4}$ | B. | $ω=\frac{π}{8}{,_{\;}}φ=\frac{π}{4}$ | C. | $ω=\frac{π}{4}{,_{\;}}φ=\frac{π}{2}$ | D. | $ω=\frac{π}{4}{,_{\;}}φ=\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 梯形 | B. | 平行四边形 | C. | 矩形 | D. | 菱形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com