考点:圆方程的综合应用
专题:综合题,直线与圆
分析:(1)将圆C化为标准方程,找出圆心与半径,作出相应的图形,所求式子表示圆上点到原点距离的平方,从而求x
2+y
2的取值范围;
(2)令
=k,则y=kx,代入圆的方程,利用△≥0,求
的最大值;
(3)
•
=(2-x,-y)•(-x,-y)=x
2+y
2-2x=2x-3,即可求
•
(O为坐标原点)的取值范围.
解答:
解:(1)圆C化为标准方程为(x-2)
2+y
2=1,圆心为(2,0),半径为1
根据图形得到P与A(3,0)重合时,离原点距离最大,此时x
2+y
2=3
2=9,P与B(1,0)重合时,离原点距离最大,此时x
2+y
2=1
2=1.
∴x
2+y
2的取值范围是[1,9];
(2)令
=k,则y=kx.
代入圆的方程,整理得(1+k
2)x
2-4x+3=0.
依题意有△=16-12(1+k
2)=4-12k
2=4(1-3k
2)≥0,即k
2-
≤0,
解得-
≤k≤
,
故
的最大值是
;
(3)
•
=(2-x,-y)•(-x,-y)=x
2+y
2-2x=2x-3,
∵1≤x≤3,
∴-1≤2x-3≤3,
∴
•
(O为坐标原点)的取值范围是[-1,3].
点评:本小题主要考查直线和圆相交,相切的有关性质,考查数形结合、化归转化的数学思想方法,以及推理论证能力、运算求解能力,属于中档题.



 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案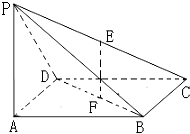 如图在四棱锥P-ABCD中,底面abcd是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=
如图在四棱锥P-ABCD中,底面abcd是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=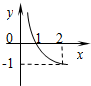 已知函数f(x)=logax(a>0,且a≠1)的图象如图所示,函数y=g(x)是函数y=f(x)的反函数,则函数y=g(x)的解析式为( )
已知函数f(x)=logax(a>0,且a≠1)的图象如图所示,函数y=g(x)是函数y=f(x)的反函数,则函数y=g(x)的解析式为( )