
【题目】设函数 ![]() .
.
(1)当a=b=2时,证明:函数f(x)不是奇函数;
(2)设函数f(x)是奇函数,求a与b的值;
(3)在(2)条件下,判断并证明函数f(x)的单调性,并求不等式 ![]() 的解集.
的解集.
【答案】
(1)解:当a=b=2时, ![]() ,
,
∵ ![]() ,f(1)=0,
,f(1)=0,
∴f(﹣1)≠﹣f(1),
∴函数f(x)不是奇函数
(2)解:由函数f(x)是奇函数,得f(﹣x)=﹣f(x),
即 ![]() 对定义域内任意实数x都成立,
对定义域内任意实数x都成立,
整理得(2a﹣b)22x+(2ab﹣4)2x+(2a﹣b)=0对定义域内任意实数x都成立,
∴ ![]() ,
,
解得 ![]() 或
或 ![]()
经检验 ![]() 符合题意
符合题意
(3)解:由(2)可知 ![]()
易判断f(x)为R上的减函数,
证明:∵2x+1在定义域R上单调递增且2x+1>0,
∴ ![]() 在定义域R上单调递减,且
在定义域R上单调递减,且 ![]() >0,
>0,
∴ ![]() 在R上单调递减.
在R上单调递减.
由 ![]() ,不等式
,不等式 ![]() ,
,
等价为f(x)>f(1),
由f(x)在R上的减函数可得x<1.
另解:由 ![]() 得,即
得,即 ![]() ,
,
解得2x<2,∴x<1.
即不等式的解集为(﹣∞,1)
【解析】(1)根据函数奇偶性的定义进行判断函数f(x)不是奇函数;(2)根据奇函数的性质建立方程即可求a与b的值;(3)根据函数单调性的定义或性质证明函数f(x)的单调性,并利用单调性的性质解不等式 ![]() .
.
【考点精析】利用函数单调性的性质和函数的奇偶性对题目进行判断即可得到答案,需要熟知函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集;偶函数的图象关于y轴对称;奇函数的图象关于原点对称.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】一个袋子内装有2个绿球,3个黄球和若干个红球(所有球除颜色外其他均相同),从中一次性任取2个球,每取得1个绿球得5分,每取得1个黄球得2分,每取得1个红球得1分,用随机变量![]() 表示2个球的总得分,已知得2分的概率为
表示2个球的总得分,已知得2分的概率为![]() .
.
(Ⅰ)求袋子内红球的个数;
(Ⅱ)求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义域为R的偶函数,当x≥0时,f(x)= 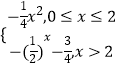 ,若关于x的方程[f(x)]2+af(x)+
,若关于x的方程[f(x)]2+af(x)+ ![]() =0,a∈R有且仅有8个不同实数根,则实数a的取值范围是
=0,a∈R有且仅有8个不同实数根,则实数a的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间[0,a]上的函数f(x)的图象如图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形的面积为S(x),则函数S(x)的导函数S′(x)的图象大致是( ) 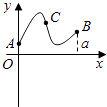
A.
B.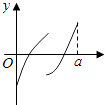
C.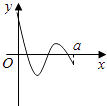
D.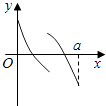
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,数列{bn},{cn}满足 (n+1) bn=an+1![]() ,(n+2) cn=
,(n+2) cn=![]() ,其中n∈N*.
,其中n∈N*.
(1)若数列{an}是公差为2的等差数列,求数列{cn}的通项公式;
(2)若存在实数λ,使得对一切n∈N*,有bn≤λ≤cn,求证:数列{an}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,然后在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒(如图).设小正方形边长为x厘米,矩形纸板的两边AB,BC的长分别为a厘米和b厘米,其中a≥b.
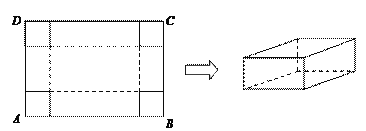
(1)当a=90时,求纸盒侧面积的最大值;
(2)试确定a,b,x的值,使得纸盒的体积最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家公司计划生产某种小型产品的月固定成本为1万元,每生产1万件需要再投入2万元,设该公司一个月内生产该小型产品x万件并全部销售完,每万件的销售收入为4﹣x万元,且每万件国家给予补助2e﹣ ![]() ﹣
﹣ ![]() 万元.(e为自然对数的底数,e是一个常数)
万元.(e为自然对数的底数,e是一个常数)
(1)写出月利润f(x)(万元)关于月产量x(万件)的函数解析式
(2)当月产量在[1,2e]万件时,求该公司在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生成量值(万件).(注:月利润=月销售收入+月国家补助﹣月总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+(1﹣a) x2﹣a(a+2)x+b(a,b∈R).
(1)若函数f(x)的图象过原点,且在原点处的切线斜率是﹣3,求a,b的值;
(2)若函数f(x)在区间(﹣1,1)上不单调,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com