练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数.

    （1）讨论的单调性；

    （2）若，设，证明：，，使.

    【答案】（1）见解析；（2）证明见解析.

    【解析】

    （1），分，，，四种情况讨论即可；

    （2）问题转化为，利用导数找到与即可证明.

    （1）.

    ①当时，恒成立，

    当时，；

    当时，，所以，

    在上是减函数，在上是增函数.

    ②当时，，.

    当时，；

    当时，；

    当时，，所以，

    在上是减函数，在上是增函数，

    在上是减函数.

    ③当时，，

    则在上是减函数.

    ④当时，，

    当时，；

    当时，；

    当时，，

    所以，在上是减函数，

    在上是增函数，在上是减函数.

    （2）由题意，得.

    由（1）知，当，时，，

    .

    令，，

    故在上是减函数，有，

    所以，从而.

    ，，

    则，

    令，显然在上是增函数，

    且，，

    所以存在使，

    且在上是减函数，

    在上是增函数，

    ，

    所以，

    所以，命题成立.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某公司甲、乙两个班组分别试生产同一种规格的产品，已知此种产品的质量指标检测分数不小于70时，该产品为合格品，否则为次品，现随机抽取两个班组生产的此种产品各100件进行检测，其结果如下表：

    质量指标检测分数

    [50，60）

    [60，70）

    [70，80）

    [80，90）

    [90，100]

    甲班组生产的产品件数

    7

    18

    40

    29

    6

    乙班组生产的产品件数

    8

    12

    40

    32

    8

    （1）根据表中数据，估计甲、乙两个班组生产该种产品各自的不合格率；

    （2）根据以上数据，完成下面的2×2列联表，并判断是否有95％的把握认为该种产品的质量与生产产品的班组有关？

    甲班组

    乙班组

    合计

    合格品

    次品

    合计

    （3）若按合格与不合格比例，从甲班组生产的产品中抽取4件产品，从乙班组生产的产品中抽取5件产品，记事件A：从上面4件甲班组生产的产品中随机抽取2件，且都是合格品；事件B：从上面5件乙班组生产的产品中随机抽取2件，一件是合格品，一件是次品，试估计这两个事件哪一种情况发生的可能性大．

    附：

    P（K2≥k）

    0.050

    0.010

    0.001

    k

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，是边长为4的正方形，平面，分别为的中点.

    （1）证明：平面.

    （2）若，求二面角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有下列命题：

    ①函数与的图象关于轴对称；

    ②若函数，则，都有；

    ③若函数，在上单调递增，则；

    ④若函数，则函数的最小值为．

    其中真命题的序号是______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥的底面ABCD是边长为2的正方形，且.若四棱锥P-ABCD的五个顶点在以4为半径的同一球面上，当PA最长时，则______________；四棱锥P-ABCD的体积为______________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面是平行四边形，，平面底面，且，，分别为，的中点.

    （1）求证：平面；

    （2）求证：平面平面；

    （3）求三棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下图是某机械零件的几何结构，该几何体是由两个相同的直四棱柱组合而成的，且前后，左右、上下均对称，每个四棱柱的底面都是边长为2的正方形，高为4，且两个四棱柱的侧棱互相垂直.则这个几何体的体积为________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线l的参数方程为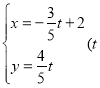为参数），以原点O为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为ρ＝asinθ（a≠0）.

    （1）求圆C的直角坐标方程与直线l的普通方程；

    （2）设直线l截圆C的弦长是半径长的倍，求a的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】《山东省高考改革试点方案》规定：从2017年秋季高中入学的新生开始，不分文理科；2020年开始，高考总成绩由语数外3门统考科目和物理、化学等六门选考科目构成.将每门选考科目的考生原始成绩从高到低划分为A、B+、B、C+、C、D+、D、E共8个等级.参照正态分布原则，确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%.选考科目成绩计入考生总成绩时，将A至E等级内的考生原始成绩，依照等比例转换法则，分别转换到[91,100]、[81,90]、[71,80]、[61,70]、[51,60]、[41,50]、[31,40]、[21,30]八个分数区间，得到考生的等级成绩．

    某校高一年级共2000人，为给高一学生合理选科提供依据，对六个选考科目进行测试，其中物理考试原始成绩基本服从正态分布N（60,169）．

    （Ⅰ）求物理原始成绩在区间（47,86）的人数；

    （Ⅱ）按高考改革方案，若从全省考生中随机抽取3人，记X表示这3人中等级成绩在区间[61,80]的人数，求X的分布列和数学期望.

    （附：若随机变量，则，，）

    查看答案和解析>>

    同步练习册答案