
【题目】在三棱锥A﹣BCD中,△ABC和△ABD都是以AB为斜边的直角三角形,AB⊥CD,AB=10,CD=6.
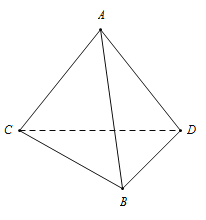
(1)问在AB上是否存在点E,使得AB⊥平面ECD?
(2)如果S△ABC=S△ABD=30,求二面角C﹣AB﹣D的大小.
(3)求三棱锥A﹣BCD体积的最大值.
【答案】(1)见解析;(2)60°;(3)40
【解析】
(1)利用线面垂直的判定方法可得;
(2)根据两个三角形面积相等可得DE,CE的长度,从而可得二面角;
(3)求出三棱锥A﹣BCD体积的表达式,利用二次函数知识可得.
(1)假设在AB上存在点E,使得AB⊥平面ECD,
∵在三棱锥A﹣BCD中,△ABC和△ABD都是以AB为斜边的直角三角形,
AB⊥CD,AB=10,CD=6.作CE⊥AB,交AB于E,连结DE,
又CE∩CD=C,∴AB⊥平面ECD.
(2)由(1)知AB⊥平面CDE,故AB⊥DE,AB⊥CE,∴CED为二面角C﹣AB﹣D的平面角,
∵AB=10, S△ABC=S△ABD=30,∴![]() ,
,
解得DE=CE=6,又CD=6,∴△CDE是等边三角形,∴∠CED=60°,
即二面角C﹣AB﹣D的大小为60°.
(3)由(1)知AB⊥平面CDE,故VA﹣BCD=![]() S△CDEAB=
S△CDEAB=![]() S△CDE,
S△CDE,
∵△ABD和△ABC都是以AB为斜边的直角三角形,且由(1)知AB⊥平面CDE,
∴CE=DE,设CE=DE=m,则E到CD的距离d=![]() ,∴S△CDE=
,∴S△CDE=![]() ,
,
∵△ABD是直角三角形,∴D在以AB为直径的圆上,故DE的最大值为![]() AB=5,
AB=5,
即0<m≤5,∴S△CDE的最大值为![]() 12,
12,
∴三棱锥A﹣BCD体积的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】中国海军,正在以不可阻挡的气魄向深蓝进军.在中国海军加快建设的大背景下,国产水面舰艇吨位不断增大、技术日益现代化,特别是国产航空母舰下水,航母需要大量高素质航母舰载机飞行员.为此中国海军在全国9省9所优质普通高中进行海航班建设试点培育航母舰载机飞行员.2017年4月我省首届海军航空实验班开始面向全省遴选学员,有10000名初中毕业生踊跃报名投身国防,经过文化考试、体格测试、政治考核、心理选拔等过程筛选,最终招收50名学员.培养学校在关注学员的文化素养同时注重学员的身体素质,要求每月至少参加一次野营拉练活动(下面简称“活动”),这批海航班学员在10月参加活动的次数统计如图所示:
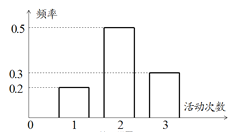
(1)从海航班学员中任选2名学员,求他们10月参加活动次数恰好相等的概率;
(2)从海航班学员中任选2名学员,用![]() 表示这两学员10月参加活动次数之差绝对值,求随机变量
表示这两学员10月参加活动次数之差绝对值,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中盈不足章中有这样一则故事:“今有良马与驽马发长安,至齐. 齐去长安三千里. 良马初日行一百九十三里,日增一十二里;驽马初日行九十七里,日减二里.” 为了计算每天良马和驽马所走的路程之和,设计框图如下图. 若输出的 ![]() 的值为 360,则判断框中可以填( )
的值为 360,则判断框中可以填( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线C的顶点在坐标原点,对称轴为x轴,抛物线C过点A(4,4),过抛物线C的焦点F作倾斜角等于45°的直线l,直线l交抛物线C于M、N两点.
(1)求抛物线C的方程;
(2)求线段MN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像经过点
的图像经过点![]() ,且
,且![]() 的相邻两个零点的距离为
的相邻两个零点的距离为![]() ,为得到
,为得到![]() 的图像,可将
的图像,可将![]() 图像上所有点( )
图像上所有点( )
A.先向右平移![]() 个单位,再将所得图像上所有点的横坐标缩短为原来的
个单位,再将所得图像上所有点的横坐标缩短为原来的![]() ,纵坐标不变
,纵坐标不变
B.先向左平移![]() 个单位,再将所得图像上所有点的横坐标缩短为原来的
个单位,再将所得图像上所有点的横坐标缩短为原来的![]() ,纵坐标不变
,纵坐标不变
C.先向左平移![]() 个单位,再将所得图像上所有点的横坐标伸长为原来的2倍,纵坐标不变
个单位,再将所得图像上所有点的横坐标伸长为原来的2倍,纵坐标不变
D.先向右平移![]() 个单位,再将所得图像上所有点的横坐标伸长为原来的2倍,纵坐标不变
个单位,再将所得图像上所有点的横坐标伸长为原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频数分布表和频率分布直方图,将使用手机时间不低于80分钟的学生称为“手机迷”.

高一学生日均使用手机时间的频数分布表
时间分组 | 频数 |
[0,20) | 12 |
[20,40) | 20 |
[40,60) | 24 |
[60,80) | 18 |
[80,100) | 22 |
[100,120] | 4 |
(1)将频率视为概率,估计哪个年级的学生是“手机迷”的概率大?请说明理由.
(2)在高二的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
非手机迷 | 手机迷 | 合计 | |
男 | |||
女 | |||
合计 |
附:随机变量 (其中
(其中![]() 为样本总量).
为样本总量).
参考数据 |
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥 P - ABCD 中,锐角三角形 PAD 所在平面垂直于平面 PAB,AB⊥AD,AB⊥BC。

(1) 求证:BC∥平面 PAD;
(2) 平面 PAD⊥ 平面 ABCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() ,k≠0,k∈R.
,k≠0,k∈R.
(1)讨论函数f(x)的奇偶性,并说明理由;
(2)已知f(x)在(﹣∞,0]上单调递减,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com