
【题目】已知关于![]() 的不等式
的不等式![]() 有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数
有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数![]() 的取值范围是( )
的取值范围是( )
A. (![]() ,
,![]() ] B. (
] B. (![]() ,
,![]() ] C. [
] C. [![]() ,
,![]() ) D. [
) D. [![]() ,
,![]() )
)
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,
,![]() 是以
是以![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形,![]() 为线段
为线段![]() 的中点,
的中点,![]() 是
是![]() 的中点,
的中点,![]() 与
与![]() 分别是以
分别是以![]() 、
、![]() 为底边的等边三角形,现将
为底边的等边三角形,现将![]() 与
与![]() 分别沿
分别沿![]() 与
与![]() 向上折起(如图
向上折起(如图![]() ),则在翻折的过程中下列结论可能正确的个数为( )
),则在翻折的过程中下列结论可能正确的个数为( )
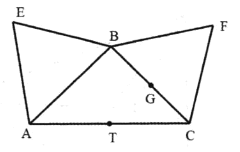
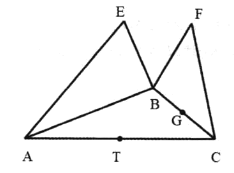
图![]() 图
图![]()
(1)直线![]() 直线
直线![]() ;(2)直线
;(2)直线![]() 直线
直线![]() ;
;
(3)平面![]() 平面
平面![]() ;(4)直线
;(4)直线![]() 直线
直线![]() .
.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
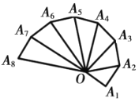
【题目】如图是第七届国际数学教育大会的会徽,它的主题图案由一连串如图所示的直角三角形演化而成.设其中的第一个直角![]() 是等腰三角形,且
是等腰三角形,且![]() ,则,
,则,![]() ,现将
,现将![]() 沿
沿![]() 翻折成
翻折成![]() ,则当四面体
,则当四面体![]() 体积最大时,它的表面有________个直角三角形;当
体积最大时,它的表面有________个直角三角形;当![]() 时,四面体
时,四面体![]() 外接球的体积为________.
外接球的体积为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网购人数的日益增多,网上的支付方式也呈现一种多样化的状态,越来越多的便捷移动支付方式受到了人们的青睐,更被网友们评为“新四大发明”之一.随着人们消费观念的进步,许多人喜欢用信用卡购物,考虑到这一点,一种“网上的信用卡”横空出世——蚂蚁花呗.这是一款支付宝和蚂蚁金融合作开发的新支付方式,简单便捷,同时也满足了部分网上消费群体在支付宝余额不足时的“赊购”消费需求.为了调查使用蚂蚁花呗“赊购”消费与消费者年龄段的关系,某网站对其注册用户开展抽样调查,在每个年龄段的注册用户中各随机抽取100人,得到各年龄段使用蚂蚁花呗“赊购”的人数百分比如图所示.
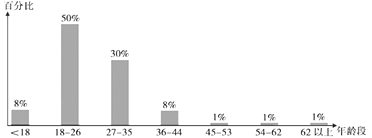
(1)由大数据可知,在18到44岁之间使用花呗“赊购”的人数百分比y与年龄x成线性相关关系,利用统计图表中的数据,以各年龄段的区间中点代表该年龄段的年龄,求所调查群体各年龄段“赊购”人数百分比y与年龄x的线性回归方程(回归直线方程的斜率和截距保留两位有效数字);
(2)该网站年龄为20岁的注册用户共有2000人,试估算该网站20岁的注册用户中使用花呗“赊购”的人数;
(3)已知该网店中年龄段在18-26岁和27-35岁的注册用户人数相同,现从18到35岁之间使用花呗“赊购”的人群中按分层抽样的方法随机抽取8人,再从这8人中简单随机抽取2人调查他们每个月使用花呗消费的额度,求抽取的两人年龄都在18到26岁的概率.
参考答案: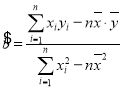 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,直角梯形![]() 中,
中,![]() ,
,![]() ,E、F分别是
,E、F分别是![]() 和
和![]() 上的点,且
上的点,且![]() ,
,![]() ,
,![]() ,沿
,沿![]() 将四边形
将四边形![]() 折起,如图2,使
折起,如图2,使![]() 与
与![]() 所成的角为60°.
所成的角为60°.
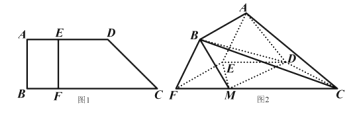
(1)求证:![]() 平面
平面![]() ;
;
(2)M为![]() 上的点,
上的点,![]() ,若二面角
,若二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据《环境空气质量指数![]() 技术规定(试行)》规定:空气质量指数在区间
技术规定(试行)》规定:空气质量指数在区间![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 时,其对应的空气质量状况分别为优、良、轻度污染、中度污染、重度污染、严重污染.如图为某市2019年10月1日至10月7日的空气质量指数
时,其对应的空气质量状况分别为优、良、轻度污染、中度污染、重度污染、严重污染.如图为某市2019年10月1日至10月7日的空气质量指数![]() 直方图,在这7天内,下列结论正确的是( )
直方图,在这7天内,下列结论正确的是( )
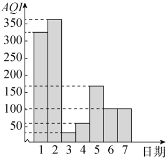
A.前4天![]() 的方差小于后3天
的方差小于后3天![]() 的方差
的方差
B.这7天内空气质量状况为严重污染的天数为3
C.这7天的平均空气质量状况为良
D.空气质量状况为优或良的概率为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com