已知方程x2+y2-2mx-4y+5m=0的曲线是圆C
(1)求m的取值范围;
(2)当m=-2时,求圆C截直线l:2x-y+1=0所得弦长;
(3)若圆C与直线2x-y+1=0相交于M,N两点,且以MN为直径的圆过坐标原点O,求m的值?
【答案】
分析:(1)圆的方程化为标准形式,利用右侧大于0,即可求m的取值范围;
(2)当m=-2时,通过弦心距,半径,半弦长满足勾股定理,求圆C截直线l:2x-y+1=0所得弦长;
( 3)若圆C与直线2x-y+1=0相交于M,N两点,且以MN为直径的圆过坐标原点O,得到
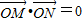
,设M(x
1,y
1),N(x
2,y
2),推出x
1x
2+y
1y
2=0,联立
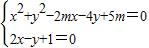
,推出x
1x
2+y
1y
2=5x
1x
2+2(x
1+x
2)+1=0,求m的值?
解答:解(1)方程x
2+y
2-2mx-4y+5m=0化为:(x-m)
2+(y-2)
2=m
2-5m+4m
2-5m+4
方程表示圆的方程,所以m
2-5m+4m
2-5m+4>0
解得:m<1或m>4;
(2)设m=-2,圆心为C(-2,2),半径R=3
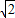
,
圆心到直线的距离为
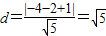
,
圆C截直线l:2x-y+1=0所得弦长为:
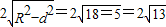
;
(3)以MN为直径的圆过坐标原点O,
即OM⊥ON
设M(x
1,y
1),N(x
2,y
2),则x
1x
2+y
1y
2=0
由
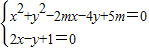
整理得 5x
2-(2m+4)x+5m-3=0,
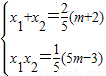
,
x
1x
2+y
1y
2=5x
1x
2+2(x
1+x
2)+1=0,
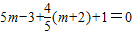
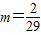
经检验,此时△=(2m+4)
2-20(5m-3)>0
∴
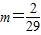 点评:
点评:本题考查直线与圆的位置故选,圆的方程的判断,考查函数与方程的思想,转化思想.设而不求的解题方法,考查计算能力.

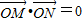 ,设M(x1,y1),N(x2,y2),推出x1x2+y1y2=0,联立
,设M(x1,y1),N(x2,y2),推出x1x2+y1y2=0,联立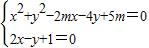 ,推出x1x2+y1y2=5x1x2+2(x1+x2)+1=0,求m的值?
,推出x1x2+y1y2=5x1x2+2(x1+x2)+1=0,求m的值?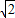 ,
,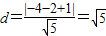 ,
,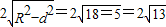 ;
;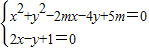
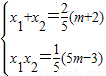 ,
,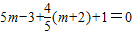
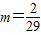
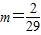


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案