电视台在某企业的赞助下,播放两套电视连续剧,其中连续剧甲每次播放时间为80分钟,广告时间为1分钟,收视观众为60万,连续剧乙每次的播放时间为40分钟,广告时间为1分钟,收视观众为20万,已知该企业与电视台所签协议要求电视台每周至少播放6分钟的广告,而电视台每周只能为该企业提供不多于320分钟的节目时间,问电视台每周应播放两套电视连续剧各多少次,才能使收视观众最多?
解:将所给信息用下表表示.

设每周播放连续剧甲x次,播放连续剧乙y次,收视率为z.
则目标函数为z=60x+20y,
约束条件为
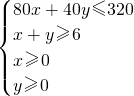
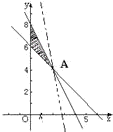
,作出可行域如图.(5分)
作平行直线系y=-3x+
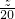
,由图可知,当直线过点A时纵截距
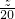
最大.(6分)
解方程组
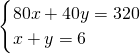
,得点A的坐标为(2,4),z
max=60x+20y=200(万).(11分)
所以,电视台每周应播放连续剧甲2次,播放连续剧乙4次,才能获得最高的收视率.
分析:先设每周播放连续剧甲x次,播放连续剧乙y次,收视率为z.写出约束条件与目标函数,欲求两套连续剧各播多少次,才能获得最高的收视率,即求可行域中的最优解,在线性规划的解答题中建议使用直线平移法求出最优解,即将目标函数看成是一条直线,分析目标函数Z与直线截距的关系,进而求出最优解.
点评:在解决线性规划的应用题时,其步骤为:①分析题目中相关量的关系,列出不等式组,即约束条件?②由约束条件画出可行域?③分析目标函数Z与直线截距之间的关系?④使用平移直线法求出最优解?⑤还原到现实问题中.属于基础题.


 设每周播放连续剧甲x次,播放连续剧乙y次,收视率为z.
设每周播放连续剧甲x次,播放连续剧乙y次,收视率为z.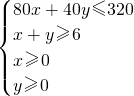 ,作出可行域如图.(5分)
,作出可行域如图.(5分)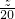 ,由图可知,当直线过点A时纵截距
,由图可知,当直线过点A时纵截距 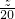 最大.(6分)
最大.(6分)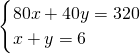 ,得点A的坐标为(2,4),zmax=60x+20y=200(万).(11分)
,得点A的坐标为(2,4),zmax=60x+20y=200(万).(11分)
