
【题目】设函数f(x)=kx2﹣kx,g(x)= ![]() ,若使得不等式f(x)≥g(x)对一切正实数x恒成立的实数k存在且唯一,则实数a的值为 .
,若使得不等式f(x)≥g(x)对一切正实数x恒成立的实数k存在且唯一,则实数a的值为 .
【答案】2
【解析】解:由题意:函数f(x)=,g(x)= ![]() ,
,
当g(x)=lnx(x≥1),图象过(1,0),使得不等式f(x)≥g(x)对一切正实数x恒成立的实数k存在且唯一,即kx2﹣kx﹣lnx≥0,令m(x)=kx2﹣kx﹣lnx≥0
则m′(x)=2kx﹣k﹣ ![]() ≥0.
≥0.
实数k存在且唯一,当x=1时,解得k=1.
即k=1.可得函数f(x)=x2﹣x.
当0<x<1时,要使f(x)≥g(x)对一切正实数x恒成立,即x2﹣x≥﹣x3+(a+1)x2﹣ax.
令h(x)=x2﹣ax+a﹣1≥0,
∵对一切正实数x恒成立且唯一,
∴△=a2﹣4(a﹣1)=0,
解得:a=2.
所以答案是:2.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知3acosA=ccosB+bcosC.
(1)求cosA,sinA的值;
(2)若cosB+cosC= ![]() ,求cosC+
,求cosC+ ![]() sinC的值.
sinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=6cos2 ![]() +
+ ![]() sinωx﹣3(ω>2)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且ABC为正三角形.
sinωx﹣3(ω>2)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且ABC为正三角形. 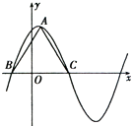
(1)求ω的值;
(2)求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0),离心率为
=1(a>b>0),离心率为 ![]() ,左准线方程是x=﹣2,设O为原点,点A在椭圆C上,点B在直线y=2上,且OA⊥OB.
,左准线方程是x=﹣2,设O为原点,点A在椭圆C上,点B在直线y=2上,且OA⊥OB. 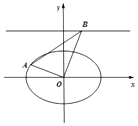
(1)求椭圆C的方程;
(2)求△AOB面积取得最小值时,线段AB的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的顶点在原点,过点A(-4,4)且焦点在x轴.
(1)求抛物线方程;
(2)直线l过定点B(-1,0)与该抛物线相交所得弦长为8,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}为等差数列,数列{bn}为等比数列.若a1<a2 , b1<b2 , 且bi=ai2(i=1,2,3),则数列{bn}的公比为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解甲、乙两所学校全体高三年级学生在该地区八校联考中的数学成绩情况,从两校各随机抽取60名学生,将所得样本作出频数分布统计表如下: 甲校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 2 | 5 | 9 | 10 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 14 | 10 | 6 | 4 |
乙校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 2 | 4 | 8 | 16 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 15 | 6 | 6 | 3 |
以抽样所得样本数据估计总体
(1)比较甲、乙两校学生的数学平均成绩的高低;
(2)若规定数学成绩不低于120分为优秀,从甲、乙两校全体高三学生中各随机抽取2人,其中数学成绩为优秀的共X人,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的半径为2,圆心在
的半径为2,圆心在![]() 轴的正半轴上,且与直线
轴的正半轴上,且与直线![]() 相切.
相切.
(1)求圆![]() 的方程。
的方程。
(2)在圆![]() 上,是否存在点
上,是否存在点![]() ,使得直线
,使得直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,且△
,且△![]() 的面积最大?若存在,求出点
的面积最大?若存在,求出点![]() 的坐标及对应的△
的坐标及对应的△![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com