
已知函数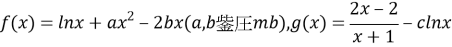 .
.
(1当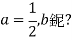 时,
时,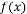 与
与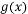 )在定义域上单调性相反,求的
)在定义域上单调性相反,求的 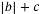 的最小值。
的最小值。
(2)当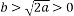 时,求证:存在
时,求证:存在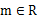 ,使
,使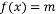 的三个不同的实数解
的三个不同的实数解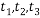 ,且对任意
,且对任意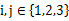 且
且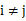 都有
都有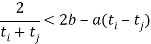 .
.
(1) 1,(2)详见解析.
【解析】
试题分析:(1)利用导数求函数单调性,注意考虑函数定义域. 两个函数的单调性可以从可以确定的函数入手.因为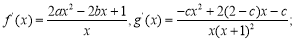 当
当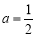 时,
时, ;当
;当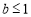 时,
时,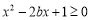 对
对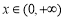 恒成立,所以,
恒成立,所以,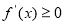 对
对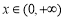 恒成立,所以,
恒成立,所以,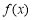 在
在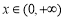 上为增函数。根据
上为增函数。根据 和
和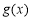 在定义域上单调性相反得,
在定义域上单调性相反得,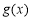 在
在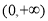 上为减函数,所以
上为减函数,所以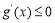 对
对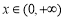 恒成立,即:
恒成立,即: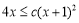 ,所以
,所以 因为
因为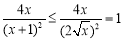 ,当且仅当
,当且仅当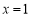 时,
时,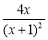 取最大值
取最大值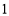 .所以
.所以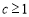 ,此时
,此时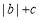 的最小值是
的最小值是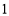 ,-(2)运用函数与方程思想,方程有三个不同的解,实质就是函数
,-(2)运用函数与方程思想,方程有三个不同的解,实质就是函数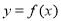 与
与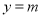 有三个不同的交点 ,由图像可知
有三个不同的交点 ,由图像可知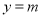 在极大值与极小值之间. 证明不等式
在极大值与极小值之间. 证明不等式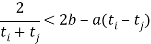 ,需从结构出发,利用条件消去a,b,将其转化为一元函数:
,需从结构出发,利用条件消去a,b,将其转化为一元函数: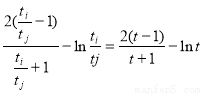 ,从而根据函数
,从而根据函数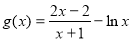 单调性,证明不等式.
单调性,证明不等式.
解析:(1)因为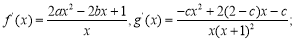 2分。
2分。
当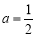 时,
时, ;当
;当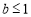 时,
时,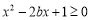 对
对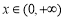 恒成立,
恒成立,
所以,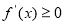 对
对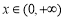 恒成立,所以,
恒成立,所以,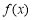 在
在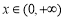 上为增函数。
上为增函数。
根据 和
和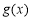 在定义域上单调性相反得,
在定义域上单调性相反得,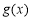 在
在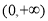 上为减函数,所以
上为减函数,所以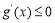 对
对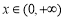 恒成立,即:
恒成立,即: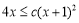 ,所以
,所以 因为
因为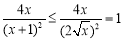 ,当且仅当
,当且仅当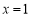 时,
时,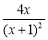 取最大值
取最大值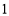 .所以
.所以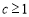 ,此时
,此时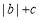 的最小值是
的最小值是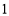 , 6分
, 6分
(2)因为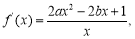 当
当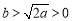 时,
时,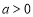 ,且一元二次方程
,且一元二次方程 的
的 ,所以
,所以 有两个不相等的实根
有两个不相等的实根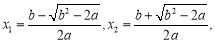 8分
8分
当 时,
时, 为增函数;
为增函数;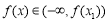
当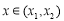 时,
时, 为减函数;
为减函数;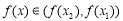
当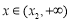 时,
时, 为增函数;
为增函数;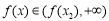
所以当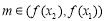 时,
时,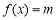 一定有3个不相等的实根
一定有3个不相等的实根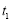 ,
,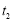 ,
,
分别在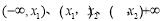 内,不妨设
内,不妨设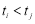 ,因为
,因为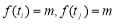 ,所以
,所以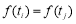 即
即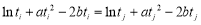 即
即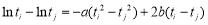
即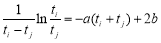 所以
所以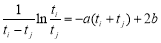
所以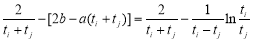
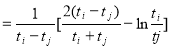
 ,令
,令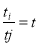 ,则
,则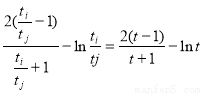
由(1)知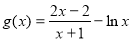 在
在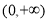 上为减函数,又
上为减函数,又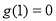
所以当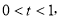

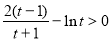 ,又
,又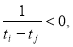
所以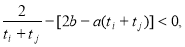 即
即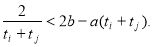 16分
16分
考点:利用导数求函数单调性,利用导数求函数交点,利用导数证明不等式


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源:2013-2014学年江苏省徐州市高三第三次质量检测文科数学试卷(解析版) 题型:填空题
一个正方体玩具的6个面分别标有数字1,2,2,3,3,3.若连续抛掷该玩具两次,则向上一面数字之和为5的概率为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高考模拟考试理科数学试卷(解析版) 题型:解答题
如图,在四棱柱 中,已知平面
中,已知平面 平面
平面 且
且 ,
, .
.
(1)求证:
(2)若 为棱
为棱 上的一点,且
上的一点,且 平面
平面 ,求线段
,求线段 的长度
的长度

查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高考模拟考试理科数学试卷(解析版) 题型:填空题
在不等式组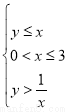 ,所表示的平面区域内的所有格点(横、纵坐标均为整数的点称为格点)中任取3个点,则该3点恰能作为一个三角的三个顶点的概率为 .
,所表示的平面区域内的所有格点(横、纵坐标均为整数的点称为格点)中任取3个点,则该3点恰能作为一个三角的三个顶点的概率为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高考模拟考试文科数学试卷(解析版) 题型:填空题
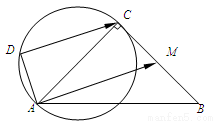
如图,已知:|AC|=|BC|=4,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则 的最大值是 .
的最大值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com