
【题目】为方便市民休闲观光,市政府计划在半径为200米,圆心角为120°的扇形广场内(如图所示),沿△ABC边界修建观光道路,其中A、B分别在线段CP、CQ上,且A、B两点间距离为定长 ![]() 米.
米. 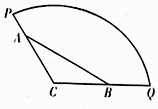
(1)当∠BAC=45°时,求观光道BC段的长度;
(2)为提高观光效果,应尽量增加观光道路总长度,试确定图中A、B两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
科目:高中数学 来源: 题型:
【题目】已知函数f(x),定义 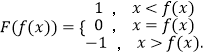
(Ⅰ)写出函数F(2x﹣1)的解析式;
(Ⅱ)若F(|x﹣a|)+F(2x﹣1)=0,求实数a的值;
(Ⅲ)当 ![]() 时,求h(x)=cosxF(x+sinx)的零点个数和值域.
时,求h(x)=cosxF(x+sinx)的零点个数和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD与AB垂直,并与AB相交于点E,点F为弦CD上异于点E的任意一点,连接BF、AF并延长交⊙O于点M、N. 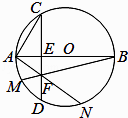
(1)求证:B、E、F、N四点共圆;
(2)求证:AC2+BFBM=AB2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为: 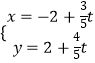 (t为参数),它与曲线C:(y﹣2)2﹣x2=1交于A,B两点.
(t为参数),它与曲线C:(y﹣2)2﹣x2=1交于A,B两点.
(1)求|AB|的长;
(2)在以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为 ![]() ,求点P到线段AB中点M的距离.
,求点P到线段AB中点M的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂准备生产甲、乙两种适销产品,每件销售收入分别为3千元,2千元.甲、乙产品都需要在A,B两种设备上加工,在每台A,B上加工一件甲产品所需工时分别为1小时、2小时,加工一件乙产品所需工时分别为2小时、1小时,A、B两种设备每月有效使用台时数分别为400小时和500小时.如何安排生产可使月收入最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项等比数列{an}的前n项和为Sn , 且a2a3=a5 , S4=10S2 .
(1)求数列{an}的通项公式;
(2)设bn=(2n﹣1)an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是各项均为正整数的等差数列,公差d∈N* , 且{an}中任意两项之和也是该数列中的一项.
(1)若a1=4,则d的取值集合为;
(2)若a1=2m(m∈N*),则d的所有可能取值的和为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com