
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2.
,如图2.
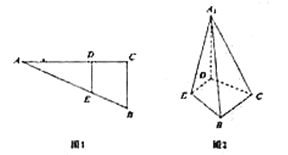
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)当![]() 长为多少时,异面直线
长为多少时,异面直线![]() ,
,![]() 所成的角最小,并求出此时所成角的余弦值.
所成的角最小,并求出此时所成角的余弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() 的参数方程为
的参数方程为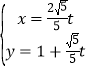 (
(![]() 为参数,且
为参数,且![]() ).
).
(1)以曲线![]() 上的点与原点
上的点与原点![]() 连线的斜率
连线的斜率![]() 为参数,写出曲线
为参数,写出曲线![]() 的参数方程;
的参数方程;
(2)若曲线![]() 与
与![]() 的两个交点为
的两个交点为![]() ,直线
,直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,记录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是 ( )
2017 2016 2015 2014……6 5 4 3 2 1
4033 4031 4029…………11 9 7 5 3
8064 8060………………20 16 12 8
16124……………………36 28 20
………………………
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知倾斜角为
中,已知倾斜角为![]() 的直线
的直线![]() 经过点
经过点![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)写出曲线![]() 的普通方程;
的普通方程;
(2)若直线![]() 与曲线
与曲线![]() 有两个不同的交点
有两个不同的交点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司近年来特别注重创新产品的研发,为了研究年研发经费![]() (单位:万元)对年创新产品销售额
(单位:万元)对年创新产品销售额![]() (单位:十万元)的影响,对近10年的研发经费
(单位:十万元)的影响,对近10年的研发经费![]() 与年创新产品销售额
与年创新产品销售额![]() (
(![]() ,10)的数据作了初步处理,得到如图的散点图及一些统计量的值.
,10)的数据作了初步处理,得到如图的散点图及一些统计量的值.
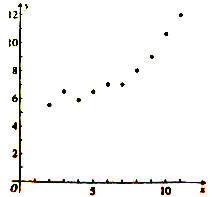
其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
现拟定![]() 关于
关于![]() 的回归方程为
的回归方程为![]() .
.
(1)求![]() ,
,![]() 的值(结果精确到0.1);
的值(结果精确到0.1);
(2)根据拟定的回归方程,预测当研发经费为13万元时,年创新产品销售额是多少?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为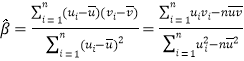 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 且
且![]() ,向量
,向量![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() .
.
(1)求函数![]() 的解析式,并求当
的解析式,并求当![]() 时,
时,![]() 的单调递增区间;
的单调递增区间;
(2)当![]() ,
,![]() 时,
时,![]() 的最大值为5,求
的最大值为5,求![]() 的值;
的值;
(3)当![]() 时,若不等式
时,若不等式![]() 在
在![]() ,
,![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数学考试中,小明的成绩在90分~100分的概率是0.18,在80分~89分的概率是0.51,在70分~79分的概率是0.15,在60分~69分的概率是0.09,在60分以下的概率是0.07,计算;
(1)小明在数学考试中取得79分以上成绩的概率;
(2)小明考试及格的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com