
【题目】△ABC的内角A、B、C所对的边分别为a,b,c. (Ⅰ)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);
(Ⅱ)若a,b,c成等比数列,且c=2a,求cosB的值.
【答案】解:(Ⅰ)∵a,b,c成等差数列, ∴a+c=2b,
由正弦定理得:sinA+sinC=2sinB,
∵sinB=sin[π﹣(A+C)]=sin(A+C),
则sinA+sinC=2sin(A+C);
(Ⅱ)∵a,b,c成等比数列,
∴b2=ac,
将c=2a代入得:b2=2a2 , 即b= ![]() a,
a,
∴由余弦定理得:cosB= ![]() =
= ![]() =
= ![]()
【解析】(Ⅰ)由a,b,c成等差数列,利用等差数列的性质得到a+c=2b,再利用正弦定理及诱导公式变形即可得证;(Ⅱ)由a,b,c成等比数列,利用等比数列的性质列出关系式,将c=2a代入表示出b,利用余弦定理表示出cosB,将三边长代入即可求出cosB的值.


科目:高中数学 来源: 题型:
【题目】右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a等于 . 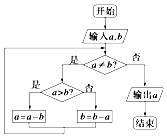
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A,B两名同学在5次数学考试中的成绩统计如下面的茎叶图所示,若A,B两人的平均成绩分别是xA , xB , 观察茎叶图,下列结论正确的是( ) 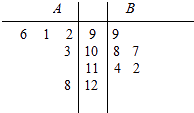
A.xA<xB , B比A成绩稳定
B.xA>xB , B比A成绩稳定
C.xA<xB , A比B成绩稳定
D.xA>xB , A比B成绩稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E﹣ABCD中,底面ABCD是矩形,AB=1,AE⊥平面CDE, ![]() ,F为线段DE上的一点.
,F为线段DE上的一点. 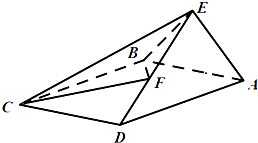
(1)求证:平面AED⊥平面ABCD;
(2)若二面角E﹣BC﹣F与二面角F﹣BC﹣D的大小相等,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com