Question

18．如图，二面角α-AB-β的大小为60°，棱上有A，B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直于AB，已知AB=4，AC=6，BD=8，则直线AB与CD所成角的余弦值为$\frac{\sqrt{17}}{17}$．

Answer 1

分析 在平面α内过B作BE∥AC，过C作CE∥AB，交BE于点E，连结DE，则∠DCE是直线AB与CD所成角或所成角的补角，由此能求出直线AB与CD所成角的余弦值．

解答 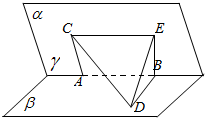解：在平面α内过B作BE∥AC，过C作CE∥AB，交BE于点E，连结DE，
∵二面角α-AB-β的大小为60°，棱上有A，B两点，
直线AC、BD分别在这个二面角的两个半平面内，
且都垂直于AB，已知AB=4，AC=6，BD=8，
∴四边形ABEC是矩形，CE=AB=4，CE∥AB，
∴∠DCE是直线AB与CD所成角或所成角的补角，
DE=$\sqrt{D{B}^{2}+B{E}^{2}}$=$\sqrt{64+36}$=10，
$\overrightarrow{CD}=\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD}$，
${\overrightarrow{CD}}^{2}$=（$\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD}$）²=${\overrightarrow{CA}}^{2}+{\overrightarrow{AB}}^{2}+{\overrightarrow{BD}}^{2}$+2$\overrightarrow{CA}•\overrightarrow{AB}$+2$\overrightarrow{CA}•\overrightarrow{BD}$+2$\overrightarrow{AB}•\overrightarrow{BD}$
=36+16+64+2×6×8×cos120°=68，
∴|$\overrightarrow{CD}$|=$\sqrt{68}$=2$\sqrt{17}$，
∴cos∠DCE=$\frac{D{C}^{2}+C{E}^{2}-D{E}^{2}}{2×DC×CE}$=$\frac{68+16-100}{2\sqrt{68}×4}$=-$\frac{\sqrt{17}}{17}$．
∴直线AB与CD所成角的余弦值为$\frac{\sqrt{17}}{17}$．

点评 本题主要考查异面直线所成角的求法，是中档题，解题时要认真审题，考查空间想象能力、运算能力和推理论证能力，属于中档题．