
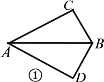
【题目】在平面四边形![]() (图①)中,
(图①)中,![]() 与
与![]() 均为直角三角形且有公共斜边
均为直角三角形且有公共斜边![]() ,设
,设![]() ,∠
,∠![]() ,∠
,∠![]() ,将
,将![]() 沿
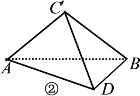
沿![]() 折起,构成如图②所示的三棱锥
折起,构成如图②所示的三棱锥![]() ,且使
,且使![]() =
=![]() .
.
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)取AB的中点O,连接![]() ,证得
,证得![]() ,从而证得C′O⊥平面ABD,再结合面面垂直的判定定理,即可证得平面
,从而证得C′O⊥平面ABD,再结合面面垂直的判定定理,即可证得平面![]() ⊥平面
⊥平面![]() ;
;
(2)以O为原点,AB,OC所在的直线为y轴,z轴,建立的空间直角坐标系,求得平面![]() 和平面
和平面![]() 的法向量,利用向量的夹角公式,即可求解.
的法向量,利用向量的夹角公式,即可求解.
(1)取AB的中点O,连接![]() ,
,![]() ,
,
在Rt△![]() 和Rt△ADB中,AB=2,则
和Rt△ADB中,AB=2,则![]() =DO=1,
=DO=1,
又C′D=![]() ,所以
,所以![]() ,即
,即![]() ⊥OD,
⊥OD,
又![]() ⊥AB,且AB∩OD=O,
⊥AB,且AB∩OD=O,![]() 平面ABD,所以
平面ABD,所以![]() ⊥平面ABD,
⊥平面ABD,
又C′O平面![]() ,所以平面
,所以平面![]() ⊥平面DAB
⊥平面DAB
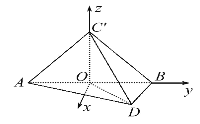
(2)以O为原点,AB,OC所在的直线为y轴,z轴,建立如图所示的空间直角坐标系,
则A(0,-1,0),B(0,1,0),C′(0,0,1), 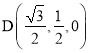 ,
,
所以![]() ,
,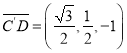 ,
,
设平面![]() 的法向量为
的法向量为![]() =(
=(![]() ),
),
则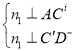 , 即
, 即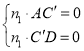 ,代入坐标得
,代入坐标得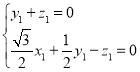 ,
,
令![]() ,得
,得![]() ,
,![]() ,所以
,所以![]() ,
,
设平面![]() 的法向量为
的法向量为![]() =(
=(![]() ),
),
则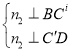 , 即
, 即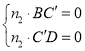 , 代入坐标得
, 代入坐标得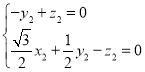 ,
,
令![]() ,得
,得![]() ,
,![]() ,所以
,所以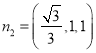 ,
,
所以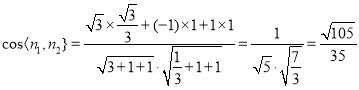 ,
,
所以二面角A-C′D-B的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】近年来,随着互联网的发展,诸如“滴滴打车”“神州专车”等网约车服务在我国各:城市迅猛发展,为人们出行提供了便利,但也给城市交通管理带来了一些困难.为掌握网约车在![]() 省的发展情况,
省的发展情况,![]() 省某调查机构从该省抽取了
省某调查机构从该省抽取了![]() 个城市,分别收集和分析了网约车的
个城市,分别收集和分析了网约车的![]() 两项指标数
两项指标数![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
|
|
|
|
|
|
|
|
|
|
|
|
经计算得: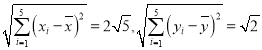
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并利用
,并利用![]() 说明
说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标数为
指标数为![]() 时,
时,![]() 指标数的估计值.
指标数的估计值.
附:相关公式: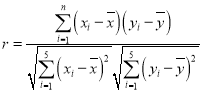 ,
,
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)曲线![]() 与曲线
与曲线![]() 有两个公共点,求实数
有两个公共点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
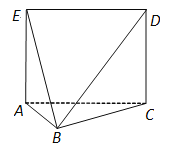
【题目】如图①,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=![]() CD=1.现以AD为一边向梯形外作正方形ADEF,然后沿边AD将正方形ADEF翻折,使平面ADEF与平面ABCD垂直,M为ED的中点,如图②.
CD=1.现以AD为一边向梯形外作正方形ADEF,然后沿边AD将正方形ADEF翻折,使平面ADEF与平面ABCD垂直,M为ED的中点,如图②.
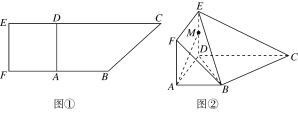
(1)求证:AM∥平面BEC;
(2)求点D到平面BEC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体![]() 中,面
中,面![]() 为矩形,面
为矩形,面![]() 面
面![]() ,
,![]() .
.
(1)求证:面![]() 面
面![]() ;
;
(2)已知多面体![]() 各顶点均在同一球面上,且该球的表面积为
各顶点均在同一球面上,且该球的表面积为![]() ,
,![]() ,当这个多面体的体积取得最大值时求其侧视图的面积.
,当这个多面体的体积取得最大值时求其侧视图的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的倾斜角为
的倾斜角为![]() ,且经过点
,且经过点![]() .以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线
.以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线![]() ,从原点O作射线交
,从原点O作射线交![]() 于点M,点N为射线OM上的点,满足
于点M,点N为射线OM上的点,满足![]() ,记点N的轨迹为曲线C.
,记点N的轨迹为曲线C.
(Ⅰ)求出直线![]() 的参数方程和曲线C的直角坐标方程;
的参数方程和曲线C的直角坐标方程;
(Ⅱ)设直线![]() 与曲线C交于P,Q两点,求
与曲线C交于P,Q两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是国家统计局于2020年1月9日发布的2018年12月到2019年12月全国居民消费价格的涨跌幅情况折线图.(注:同比是指本期与同期作对比;环比是指本期与上期作对比.如:2019年2月与2018年2月相比较称同比,2019年2月与2019年1月相比较称环比)根据该折线图,下列结论错误的是( )
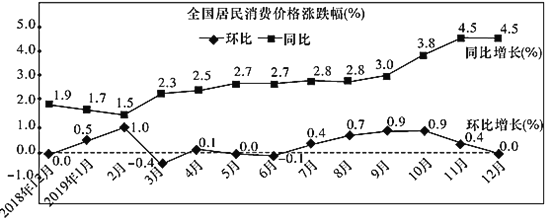
A.2019年12月份,全国居民消费价格环比持平
B.2018年12月至2019年12月全国居民消费价格环比均上涨
C.2018年12月至2019年12月全国居民消费价格同比均上涨
D.2018年11月的全国居民消费价格高于2017年12月的全国居民消费价格
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com