
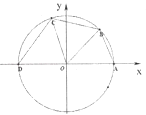
【题目】如图所示,已知点A(1,0),D(﹣1,0),点B,C在单位圆O上,且∠BOC= ![]() .
. 
(Ⅰ)若点B( ![]() ,
, ![]() ),求cos∠AOC的值;
),求cos∠AOC的值;
(Ⅱ)设∠AOB=x(0<x< ![]() ),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值.
),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值.
【答案】解:(Ⅰ)∵B( ![]() ,
, ![]() ), ∴cos∠AOB=
), ∴cos∠AOB= ![]() ,sin∠AOB=
,sin∠AOB= ![]() ;
;
∴cos∠AOC=cos(∠AOB+∠BOC)
=cos∠AOBcos∠BOC﹣sin∠AOBsin∠BOC
= ![]() ×
× ![]() ﹣
﹣ ![]() ×
× ![]()
= ![]() ;
;
(Ⅱ)等腰三角形AOB中,求得|AB|=2|OB|sin ![]() =2sin
=2sin ![]() ,
,
等腰三角形COD中,求得
|CD|=2|OC|sin 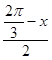 =2sin(
=2sin( ![]() ﹣
﹣ ![]() );
);
∴y=|AB|+|BC|+|CD|+|DA|
=3+2sin ![]() +2sin(
+2sin( ![]() ﹣
﹣ ![]() )
)
=3+2sin( ![]() +
+ ![]() );
);
由0<x< ![]() 得,当
得,当 ![]() +
+ ![]() =
= ![]() ,
,
即x= ![]() 时,y取得最大值5
时,y取得最大值5
【解析】(Ⅰ)由三角函数的定义,写出cos∠AOB与sin∠AOB的值,再计算cos∠AOC的值;(Ⅱ)根据等腰三角形的知识,求出|AB|、|CD|的值,再写出函数y的解析式,求出y的最大值即可.
【考点精析】解答此题的关键在于理解三角函数的最值的相关知识,掌握函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,O是坐标原点,两定点A,B满足| ![]() |=|
|=| ![]() |=
|= ![]()
![]() =2,则点集{P|
=2,则点集{P| ![]() =x
=x ![]() +y
+y ![]() ,|x|+|y|≤1,x,y∈R}所表示的区域的面积是 .
,|x|+|y|≤1,x,y∈R}所表示的区域的面积是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有三个游戏规则如表,袋子中分别装有形状、大小相同的球,从袋中无放回地取球,
游戏1 | 游戏2 | 游戏3 |
袋中装有3个黑球和2个白球 | 袋中装有2个黑球和2个白球 | 袋中装有3个黑球和1个白球 |
从袋中取出2个球 | 从袋中取出2个球 | 从袋中取出2个球 |
若取出的两个球同色,则甲胜 | 若取出的两个球同色,则甲胜 | 若取出的两个球同色,则甲胜 |
若取出的两个球不同色,则乙胜 | 若取出的两个球不同色,则乙胜 | 若取出的两个球不同色,则乙胜 |
问其中不公平的游戏是( )
A.游戏2
B.游戏3
C.游戏1和游戏2
D.游戏1和游戏3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
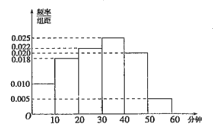
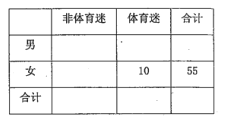
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成上面的![]() 列联表,若按
列联表,若按![]() 的可靠性要求,并据此资料,你是否认为“体育迷”与性别有关?
的可靠性要求,并据此资料,你是否认为“体育迷”与性别有关?
(2)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为![]() .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求![]() 分布列,期望
分布列,期望![]() 和方差
和方差![]() .
.
附: 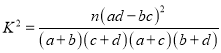

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=CD=2,PD=2![]() ,PA⊥PD,Q为PD的中点.
,PA⊥PD,Q为PD的中点.
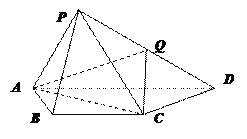
(Ⅰ)证明:CQ∥平面PAB;
(Ⅱ)求直线PD与平面AQC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为R的奇函数f(x)= ![]() ,其中h(x)是指数函数,且h(2)=4.
,其中h(x)是指数函数,且h(2)=4.
(1)求函数f(x)的解析式;
(2)求不等式f(2x﹣1)>f(x+1)的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某社区居民的家庭年收入与年支出的关系,相关部门随机调查了该社区5户家庭,得到如表统计数据表:
收入x(万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y(万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
(1)根据上表可得回归直线方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =0.76,
=0.76, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,据此估计,该社区一户年收入为15万元的家庭年支出为多少?
,据此估计,该社区一户年收入为15万元的家庭年支出为多少?
(2)若从这5个家庭中随机抽选2个家庭进行访谈,求抽到家庭的年收入恰好一个不超过10万元,另一个超过11万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cos
=(cos ![]() ,sin
,sin ![]() ),
), ![]() =(cos
=(cos ![]() ,﹣sin
,﹣sin ![]() ),且x∈[
),且x∈[ ![]() ,π].
,π].
(1)求 ![]()
![]() 及|
及| ![]() +
+ ![]() |;
|;
(2)求函数f(x)= ![]()
![]() +|
+| ![]() +
+ ![]() |的最大值,并求使函数取得最大值时x的值.
|的最大值,并求使函数取得最大值时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com