
【题目】已知![]()
(1)求函数![]() 的极值;
的极值;
(2)设![]() ,对于任意
,对于任意![]() ,总有
,总有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() 的极小值为:
的极小值为: ![]() ,极大值为:
,极大值为: ![]() (2)
(2) ![]()
【解析】试题分析:(1)先求函数的定义域,然后对函数求导,利用导数求得函数的单调区间,进而求得极值.(2)由(1)得到函数![]() 的最大值为
的最大值为![]() ,则只需
,则只需![]() .求出函数
.求出函数![]() 的导数,对
的导数,对![]() 分成
分成![]() 两类,讨论函数
两类,讨论函数![]() 的单调区间和最小值,由此求得
的单调区间和最小值,由此求得![]() 的取值范围.
的取值范围.
试题解析:
(1) 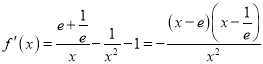

所以![]() 的极小值为:
的极小值为: ![]() ,极大值为:
,极大值为: ![]() ;
;
(2) 由(1)可知当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]()
对于任意![]() ,总有
,总有![]() 成立,等价于
成立,等价于![]() 恒成立,
恒成立,
![]()
①![]() 时,因为
时,因为![]() ,所以
,所以![]() ,即
,即![]() 在
在![]() 上单调递增,
上单调递增, ![]() 恒成立,符合题意.
恒成立,符合题意.
②当![]() 时,设
时,设![]() ,
, 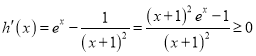 ,
,
所以![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,则存在
,则存在![]() ,使得
,使得![]()
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,又
上单调递增,又![]() ,
,
所以![]() 不恒成立,不合题意.
不恒成立,不合题意.
综合①②可知,所求实数![]() 的取值范围是
的取值范围是![]() .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元.在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费.现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
以这100台机器维修次数的频率代替1台机器维修次数发生的概率, 记![]() 表示1台机器三年内共需维修的次数,
表示1台机器三年内共需维修的次数,![]() 表示购买1台机器的同时购买的维修次数.
表示购买1台机器的同时购买的维修次数.
(1)求![]() 的分布列;
的分布列;
(2)若要求![]() ,确定
,确定![]() 的最小值;
的最小值;
(3)以在维修上所需费用的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应绿色出行,某市在推出“共享单车”后,又推出“新能源租赁汽车”.每次租车收费的标准由两部分组成:①里程计费:1元/公里;②时间计费:![]() 元/分.已知陈先生的家离上班公司
元/分.已知陈先生的家离上班公司![]() 公里,每天上、下班租用该款汽车各一次.一次路上开车所用的时间记为
公里,每天上、下班租用该款汽车各一次.一次路上开车所用的时间记为![]() (分),现统计了50次路上开车所用时间,在各时间段内频数分布情况如下表所示
(分),现统计了50次路上开车所用时间,在各时间段内频数分布情况如下表所示

将各时间段发生的频率视为概率,一次路上开车所用的时间视为用车时间,范围为![]()
![]() 分.
分.
(1)估计陈先生一次租用新能源租赁汽车所用的时间不低于![]() 分钟的概率;
分钟的概率;
(2)若公司每月发放![]() 元的交通补助费用,请估计是否足够让陈先生一个月上下班租用新能源租赁汽车(每月按
元的交通补助费用,请估计是否足够让陈先生一个月上下班租用新能源租赁汽车(每月按![]() 天计算),并说明理由.(同一时段,用该区间的中点值作代表)
天计算),并说明理由.(同一时段,用该区间的中点值作代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中志愿者部有男志愿者6人,女志愿者4人,这些人要参加元旦联欢会的服务工作. 从这些人中随机抽取4人负责舞台服务工作,另外6人负责会场服务工作.
(Ⅰ)设![]() 为事件:“负责会场服务工作的志愿者中包含女志愿者
为事件:“负责会场服务工作的志愿者中包含女志愿者![]() 但不包含男志愿者
但不包含男志愿者![]() ”,求事件
”,求事件![]() 发生的概率.
发生的概率.
(Ⅱ)设![]() 表示参加舞台服务工作的女志愿者人数,求随机变量
表示参加舞台服务工作的女志愿者人数,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为提升教师专业功底,引领青年教师成长,某市教育局举行了全市“园丁杯”课堂教学比赛,在这次比赛中,通过采用录像课评比的片区预赛,有![]() 共10位选手脱颖而出进入全市决赛.决赛采用现场上课形式,从学科评委库中采用随机抽样抽选代号1,2,3,…,7的7名评委,规则是:选手上完课,评委们当初评分,并从7位评委评分中去掉一个最高分,去掉一个最低分,根据剩余5位评委的评分,算出平均分作为该选手的最终得分.记评委
共10位选手脱颖而出进入全市决赛.决赛采用现场上课形式,从学科评委库中采用随机抽样抽选代号1,2,3,…,7的7名评委,规则是:选手上完课,评委们当初评分,并从7位评委评分中去掉一个最高分,去掉一个最低分,根据剩余5位评委的评分,算出平均分作为该选手的最终得分.记评委![]() 对某选手评分排名与该选手最终排名的差的绝对值为“评委
对某选手评分排名与该选手最终排名的差的绝对值为“评委![]() 对这位选手的分数排名偏差”
对这位选手的分数排名偏差”![]() .排名规则:由高到低依次排名,如果选手分数一样,认定名次并列(如:选手
.排名规则:由高到低依次排名,如果选手分数一样,认定名次并列(如:选手![]() 分数一致排在第二,则认为他们同属第二名,没有第三名,接下来分数为第四名).七位评委评分情况如下表所示:
分数一致排在第二,则认为他们同属第二名,没有第三名,接下来分数为第四名).七位评委评分情况如下表所示:
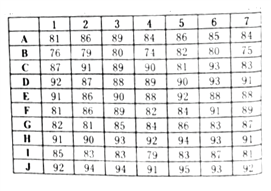
(1)根据最终评分表,填充如下表格:

(2)试借助评委评分分析表,根据评委对各选手的排名偏差的平方和,判断评委4与评委5在这次活动中谁评判更准确.
____号评委评分分析表
选手 | A | B | C | D | E | F | G | H | I | J |
最终排名 | ||||||||||
评分排名 | ||||||||||
排名偏差 |
(3)从这10位选手中任意选出3位,记其中评委4比评委5对选手排名偏差小的选手数位![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱世杰是历史上最伟大的数学家之一,他所著的![]() 四元玉鉴
四元玉鉴![]() 卷中“如像招数”五问有如下问题:“今有官司差夫一千八百六十四人筑堤
卷中“如像招数”五问有如下问题:“今有官司差夫一千八百六十四人筑堤![]() 只云初日差六十四人,次日转多七人,每人日支米三升,共支米四百三石九斗二升,问筑堤几日”
只云初日差六十四人,次日转多七人,每人日支米三升,共支米四百三石九斗二升,问筑堤几日”![]() 其大意为:“官府陆续派遣
其大意为:“官府陆续派遣![]() 人前往修筑堤坝,第一天派出
人前往修筑堤坝,第一天派出![]() 人,从第二天开始,每天派出的人数比前一天多
人,从第二天开始,每天派出的人数比前一天多![]() 人,修筑堤坝的每人每天分发大米
人,修筑堤坝的每人每天分发大米![]() 升,共发出大米
升,共发出大米![]() 升,问修筑堤坝多少天”
升,问修筑堤坝多少天”![]() 这个问题中,前
这个问题中,前![]() 天一共应发大米____________升.
天一共应发大米____________升.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() 表示
表示![]() ,
,![]() 中的最大值,如
中的最大值,如![]()
![]() .已知函数
.已知函数![]() ,
,![]() .
.
(1)设![]() ,求函数
,求函数![]() 在
在![]() 上零点的个数;
上零点的个数;
(2)试探讨是否存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com