
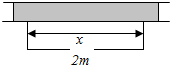 Χ��һ�����Ϊ360m2�ľ��γ��أ�Ҫ����γ��ص�һ�����þ�ǽ�����þ�ǽ��Ҫά�ޣ�����������ΧǽҪ�½����ھ�ǽ�Ķ������ǽ��Ҫ��һ������Ϊ2m�Ľ����ڣ���֪��ǽ��ά����Ϊ45Ԫ/m����ǽ�����Ϊ180Ԫ/m�������õľ�ǽ�ij���Ϊx����λ���ף������˾��γ���Χǽ���ܷ���Ϊy����λ��Ԫ����
Χ��һ�����Ϊ360m2�ľ��γ��أ�Ҫ����γ��ص�һ�����þ�ǽ�����þ�ǽ��Ҫά�ޣ�����������ΧǽҪ�½����ھ�ǽ�Ķ������ǽ��Ҫ��һ������Ϊ2m�Ľ����ڣ���֪��ǽ��ά����Ϊ45Ԫ/m����ǽ�����Ϊ180Ԫ/m�������õľ�ǽ�ij���Ϊx����λ���ף������˾��γ���Χǽ���ܷ���Ϊy����λ��Ԫ�������� ��1������ε���һ�߳�Ϊam�������Χ���ľ��γ��ص����Ϊ360m2����a=$\frac{360}{x}$����ʱ�ٸ��ݾ�ǽ��ά����Ϊ45Ԫ/m����ǽ�����Ϊ180Ԫ/m�����Ǽ��ɵõ���Χǽ���ܷ���y��ʾ��x�ĺ����Ľ���ʽ��
��2�����ݺ����ı���ʽ�������о������ĵ����ԣ�
��3�����ݣ�2����x=24ʱ�����˾��γ���Χǽ���ܷ�����С��
��� �⣺��1������ε���һ�߳�Ϊam��
��y=45x+180��x-2��+180•2a=225x+360a-360��
����֪ax=360����a=$\frac{360}{x}$��
��y=f��x��=225x+$\frac{36{0}^{2}}{x}$-360����x��2����
��2����y=f��x��=225x+$\frac{36{0}^{2}}{x}$-360����x��2����
��f'��x��=$\frac{225{x}^{2}-36{0}^{2}}{{x}^{2}}$��
����f����x����0��x��24����ʱ����������������f����x����0��2��x��24����ʱ���������ݼ���
�ʺ����ĵ�����������Ϊ��24��+�ޣ����ݼ�����Ϊ��2��24����
��3�����ݣ�2����x=24ʱ�����˾��γ���Χǽ���ܷ�����С����С�ܷ���Ϊf��x��=225x+$\frac{36{0}^{2}}{x}$-360=10440Ԫ��
���� ������Ҫ�����뺯���йص�Ӧ�����⣬������������������ϵ�ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
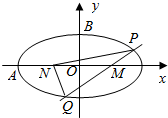 ��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������ΪA�������ΪB��M��1��0����N��n��0����|MB|=$\sqrt{2}$��|AM|=3������M��ֱ��l����x��غϣ���ֱ��l����ԲC�ཻ��P��Q���㣬����NP��NQ��
��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������ΪA�������ΪB��M��1��0����N��n��0����|MB|=$\sqrt{2}$��|AM|=3������M��ֱ��l����x��غϣ���ֱ��l����ԲC�ཻ��P��Q���㣬����NP��NQ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com