
����Ŀ�������ġ�ȼ��Ч�ʡ���ָ����ÿ����1��������ʻ����̣���ͼ�����˼ס��ҡ������������ڲ�ͬ�ٶ���ȼ��Ч�������������������ȷ���ǣ� �� 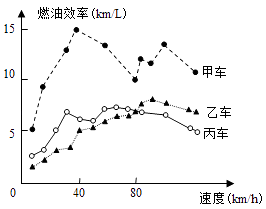
A.����1�����ͣ��ҳ�������ʻ5ǧ��
B.����ͬ�ٶ���ʻ��ͬ·�̣��������У��׳������������
C.�׳���80ǧ��/Сʱ���ٶ���ʻ1Сʱ������10������
D.ij���л������������80ǧ��/Сʱ����ͬ�����£��ڸ����ñ��������ҳ���ʡ��
���𰸡�D
���������⣺����ѡ��A����ͼ�п��Կ������ҳ�����ʻ�ٶȴ���40ǧ��ÿСʱʱ��ȼ��Ч�ʴ���5ǧ��ÿ�������ҳ�����1�����͵���ʻ·��Զ����5ǧ�ף���A����
����ѡ��B������ͬ�ٶ���ʻ��ͬ·�̣��������У��׳�����������С����B����
����ѡ��C���׳���80ǧ��/Сʱ���ٶ���ʻ1Сʱ�����Ϊ80ǧ�ף�ȼ��Ч��Ϊ10��������8�����ͣ���C����
����ѡ��D����Ϊ���ٶȵ���80ǧ��/Сʱ������ȼ��Ч�ʸ����ҵ�ȼ��Ч�ʣ���D��ȷ��
���������ġ�ȼ��Ч�ʡ���ָ����ÿ����1��������ʻ����̣��Լ�ͼ�ֱ��жϸ���ѡ��ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
�� ![]() ��
�� ![]() Ϊ��ͬ��ֱ�ߣ�
Ϊ��ͬ��ֱ�ߣ� ![]() ��
�� ![]() ��
�� ![]() ��ͬ��ƽ�棬�������ж���ȷ����()
��ͬ��ƽ�棬�������ж���ȷ����()
A. ��![]() ��
�� ![]() ��
�� ![]() ����
����![]() B. ��
B. ��![]() ��
�� ![]() ����
����![]()
C. ��![]() ��
�� ![]() ����
����![]() D. ��
D. ��![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ����
����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1���á���㷨������ͼ��ʾ�����߷�������������![]() ��һ�������ڵļ�ͼ��Ҫ���б�����㣬����ֱ������ϵ����
��һ�������ڵļ�ͼ��Ҫ���б�����㣬����ֱ������ϵ����

��2������![]() ��ͼ�����ͨ������
��ͼ�����ͨ������![]() ��ͼ������������ƽ�ơ��Ĺ���任���õ�����д��һ�������ı任��
��ͼ������������ƽ�ơ��Ĺ���任���õ�����д��һ�������ı任��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=alnx��x2+1�� ����������y=f��x����x=1�������߷���Ϊ4x��y+b=0����ʵ��a��b��ֵ��
�������ۺ���f��x���ĵ����ԣ�
������a��0���Ҷ�����x1 �� x2�ʣ�0��+�ޣ���x1��x2 �� ����|f��x1����f��x2��|��|x1��x2|����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() =
=![]() =
= ![]() ��
��
(1)����![]() �ĵ�����������;(ֻ��д�����ۼ���)
�ĵ�����������;(ֻ��д�����ۼ���)
(2)�躯��![]() =
= ![]() ,��
,��![]() ������
������![]() ����������ͬ�����,��ʵ��
����������ͬ�����,��ʵ��![]() ��ȡֵ��Χ;
��ȡֵ��Χ;
(3)������ʵ��![]() ,ʹ�ö��������
,ʹ�ö��������![]() ,����
,����![]() ����,��ʵ��
����,��ʵ��![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f(x)��cos(![]() ��x)cos(
��x)cos(![]() ��x)��g(x)��
��x)��g(x)��![]() sin 2x��
sin 2x��![]() .
.
(1)����f(x)����С�����ڣ�
(2)����h(x)��f(x)��g(x)�����ֵ������ʹh(x)ȡ�����ֵ��x�ļ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�����Σ��ı���CDEF�Ǿ��Σ���ƽ��ABCD��ƽ��CDEF����BAD=��CDA=90�㣬AB=AD=DE= ![]() CD=2��M���߶�AE�ϵĶ��㣮
CD=2��M���߶�AE�ϵĶ��㣮 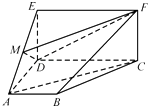
������ȷ����M��λ�ã�ʹAC��ƽ��MDF����˵�����ɣ�
�����ڣ��������£���ƽ��MDF��������ADE��BCF�ֳɵ������ֵ����֮�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ������
������![]() .
.
����![]() ʱ���ⲻ��ʽ
ʱ���ⲻ��ʽ![]() ��
��
����������![]() �ķ���
�ķ���![]() �Ľ⼯��ǡ��һ��Ԫ�أ���
�Ľ⼯��ǡ��һ��Ԫ�أ���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������![]() ����������
����������![]() ������
������![]() ������
������![]() �ϵ����ֵ����Сֵ�ĺͲ�����
�ϵ����ֵ����Сֵ�ĺͲ�����![]() ����
����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com