
���� ��PA��ƽ��ABC����PA��AC��PA��AB��PA��BC���Ӷ��õ��ĸ��涼��ֱ�������Σ�����CM����PM��ƽ��ABCʱ���õ�BM=AM=CM���Ӷ��õ�PA=PB=PC����PC��ƽ��ABCʱ��CM��ABʱ��CMȡ����Сֵ���ɴ����S��PCM����Сֵ��6�����ABC����Բ��Բ����O����PO��ƽ��ABC������OC������PO2+OC2=PC2���Ӷ������PO=$\sqrt{23}$��
��� 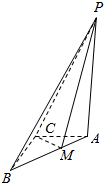 �⣺���ڢ٣���ͼ����ΪPA��ƽ��ABC������PA��AC��PA��AB��PA��BC��
�⣺���ڢ٣���ͼ����ΪPA��ƽ��ABC������PA��AC��PA��AB��PA��BC��
��BC��AC������BC��ƽ��PAC������BC��PC��
���ĸ��涼��ֱ�������Σ��ʢ���ȷ��
���ڢڣ�����CM����PM��ƽ��ABCʱ��PA2=PM2+MA2��
PB2=PM2+BM2��PC2=PM2+CM2��
��ΪM��Rt��ABCб��AB���е㣬����BM=AM=CM��
��PA=PB=PC���ʢ���ȷ��
���ڢۣ���PC��ƽ��ABCʱ��
S��PCM=$\frac{1}{2}$PC•CM=$\frac{1}{2}$��5��CM��
CM��ABʱ��CMȡ����Сֵ������Ϊ$\frac{12}{5}$��
����S��PCM����Сֵ��$\frac{1}{2}$��5��$\frac{12}{5}$=6���ʢ۴���
���ڢܣ����ABC����Բ��Բ����O����PO��ƽ��ABC������OC������PO2+OC2=PC2��
������Բ�뾶r=$\frac{1}{2}$��3+4-5��=1������OC=$\sqrt{2}$��
PO2=PC2-OC2=25-2=23����PO=$\sqrt{23}$���ʢ���ȷ��
���ϣ���ȷ�������Т٢ڢܣ�
�ʴ�Ϊ���٢ڢܣ�
���� ���⿼��������ٵ��жϣ����е��⣬����ʱҪ�������⣬ע��ռ�˼ά������������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{2}}{2}$ | B�� | 1 | C�� | $\frac{\sqrt{5}}{4}$ | D�� | $\frac{\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
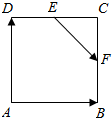
| A�� | $\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AD}$ | B�� | $\frac{1}{4}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$ | C�� | $\frac{1}{2}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AD}$ | D�� | $\frac{1}{3}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com