
(07年福建卷文)(本小题满分14分)
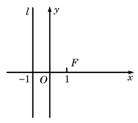
如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作l的垂线,垂足为点Q,且
![]() ?
?![]()
(I)求动点P的轨迹C的方程;
(II)过点F的直线交轨迹C于A、B两点,交直线l于点M.
(1)已知![]() 的值;
的值;
(2)求|![]() |?|
|?|![]() |的最小值.
|的最小值.
本小题考查直线、抛物线、向量等基础知识,考查轨迹方程的求法以及研究曲线几何特征的基本方法,考查运算能力和综合解题能力.满分14分.
解析:解法一:(I)设点P(x,y),则Q(-1,y),由![]() 得:
得:
(x+1,0)?(2,-y)=(x-1,y)?(-2,y),化简得C:y2=4x.

(II)(1)设直线AB的方程为:
x=my+1(m≠0).
设A(x1,y1),B(x2,y2),又M(-1,-![]() ).
).
联立方程组![]() ,消去x得:
,消去x得:
y2-4my-4=0,
△ =(-
![]()
由![]() 得:
得:
![]() ,整理得:
,整理得:
![]() ,
,
∴![]()
=![]()
=-2-![]()
=0.
解法二:(I)由![]()
∴![]() ?
?![]() ,
,
∴![]() =0,
=0,
∴![]()
所以点P的轨迹C是抛物线,由题意,轨迹C的方程为:y2=4x.
(II)(1)由已知![]()
则: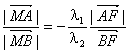 …………①
…………①
过点A、B分别作准l的垂线,垂足分别为A1、B1,
则有: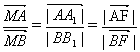 …………②
…………②
由①②得: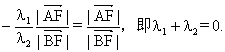
(II)(2)解:由解法一:
![]() ?
?![]() =(
=(![]() )2|y1-yM||y2-yM|
)2|y1-yM||y2-yM|
=(1+m2)|y1y2-yM(y1+y2)|+yM2|
=(1+m2)|-4+![]() ×4m+
×4m+![]() |
|
=![]()
=4(2+m2+![]() )
) ![]() 4(2+2
4(2+2![]() )=16.
)=16.
当且仅当![]() ,即m=
,即m=![]() 1时等号成立,所以
1时等号成立,所以![]() ?
?![]()
![]() 最小值为16.
最小值为16.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
(07年福建卷文)(本小题满分12分)
数列{an}的前N项和为Sn,a1=1,an+1=2Sn (n∈N*).
(I)求数列{an}的通项an;
(II)求数列{nan}的前n项和 Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
(07年福建卷文)(本小题满分12分)![]()
设函数f(x)=tx2+2t2x+t-1(x∈R,t>0).
(I)求f (x)的最小值h(t);
(II)若h(t)<-2t+m对t∈(0,2)恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(07年福建卷文)(本小题满分12分)
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(I)求证:AB1⊥平面A1BD;
(II)求二面角A-A1D-B的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
(07年福建卷文)(本小题满分12分)
甲、乙两名跳高运动员一次试跳2米高度成功的概率分别为0.7、0.6,且每次试跳成功与否相互之间没有影响,求:
(I)甲试跳三次,第三次才能成功的概率;
(II)甲、乙两人在第一次试跳中至少有一人成功的概率;
(III)甲、乙各试跳两次,甲比乙的成功次数恰好多一次的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com