
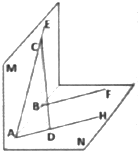
 直二面角M-AB-N中,AE、BF分别在平面M和N内,AE、BF和棱AB的夹角分别是α和β,且AB=a,求证:AE和BF的距离d=
直二面角M-AB-N中,AE、BF分别在平面M和N内,AE、BF和棱AB的夹角分别是α和β,且AB=a,求证:AE和BF的距离d=| a | ||
|
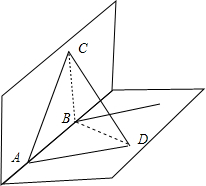 证明:过A点作BF的平行线AD,令AC=AD=a,连接BC,BD,CD
证明:过A点作BF的平行线AD,令AC=AD=a,连接BC,BD,CD| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1-cos2α•cos2β |
| V | ||
|
| ||||
|
| a | ||||
|
| a | ||||
|
| a | ||||
|
| a | ||
|
| a | ||
|


科目:高中数学 来源: 题型:
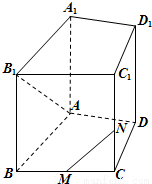
 (2010•抚州模拟)如图,在直四棱柱ABCD-A1B1C1D1中,AB=BC,∠ABC=60°,BB1=BC=2,M为BC中点,点N在CC1上.
(2010•抚州模拟)如图,在直四棱柱ABCD-A1B1C1D1中,AB=BC,∠ABC=60°,BB1=BC=2,M为BC中点,点N在CC1上.查看答案和解析>>
科目:高中数学 来源: 题型:013
∠XPB=∠YPB=45°, 那么∠XPY的大小为
[ ]
A.60° B.45° C.120° D.不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:013
在直二面角M-l-N的棱l上有两点A、B,AC![]() M,BD
M,BD![]() N,且AC⊥1,BD⊥l,AB=8cm,AC=6cm,BD=24cm,则CD等于
N,且AC⊥1,BD⊥l,AB=8cm,AC=6cm,BD=24cm,则CD等于
[ ]
A.24cm B.26cm C.28cm D.30cm
查看答案和解析>>
科目:高中数学 来源:2010年江西省抚州市高三质量检测数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com