
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
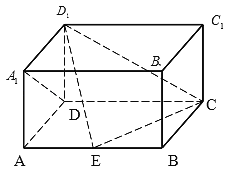
(1)证明:D1E⊥A1D;
(2)若EB![]() ,求二面角D1﹣EC﹣D的大小.
,求二面角D1﹣EC﹣D的大小.
【答案】(1)见解析(2)30°.
【解析】
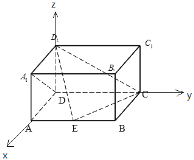
(1)以D为原点,DA,DC,DD1所在直线分别为x,y,z轴,建立空间直角坐标系,
设AE=t,(0≤t≤2),证明![]() 0即得证;(2)利用向量法求二面角D1﹣EC﹣D的大小.
0即得证;(2)利用向量法求二面角D1﹣EC﹣D的大小.
证明:(1)以D为原点,DA,DC,DD1所在直线分别为x,y,z轴,建立空间直角坐标系,
设AE=t,(0≤t≤2),则D1(0,0,1),E(1,t,0),A1(1,0,1),D(0,0,0),
![]() (1,t,﹣1),
(1,t,﹣1),![]() (﹣1,0,﹣1),
(﹣1,0,﹣1),
所以![]() 0,
0,
∴D1E⊥A1D.
(2)∵EB![]() ,∴E(1,2
,∴E(1,2![]() ,0),C(0,2,0),
,0),C(0,2,0),
![]() (1,
(1,![]() ,0),
,0),![]() (0,﹣2,1),
(0,﹣2,1),
设平面CED1的法向量![]() (x,y,z),
(x,y,z),
则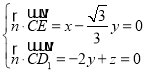 ,取y=3,得
,取y=3,得![]() (
(![]() ,6),
,6),
平面CDE的法向量![]() (0,0,1),
(0,0,1),
设二面角D1﹣EC﹣D的平面角为θ,
则cosθ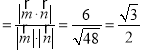 ,所以θ=30°,
,所以θ=30°,
∴二面角D1﹣EC﹣D的大小为30°.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为边长为2的菱形,
为边长为2的菱形,![]() ,
,![]() ,面
,面![]() 面
面![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.

(1)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 面
面![]() ,并说明理由;
,并说明理由;
(2)当二面角![]() 的余弦值为
的余弦值为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次的一次学科测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.

(Ⅰ)求参加测试的总人数及分数在[80,90)之间的人数;
(Ⅱ)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,恰有一份分数在[90,100)之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数![]() 与听课时间
与听课时间![]() (单位:分钟)之间的关系满足如图所示的曲线.当
(单位:分钟)之间的关系满足如图所示的曲线.当![]() 时,曲线是二次函数图象的一部分,当
时,曲线是二次函数图象的一部分,当![]() 时,曲线是函数
时,曲线是函数![]() 图象的一部分.根据专家研究,当注意力指数
图象的一部分.根据专家研究,当注意力指数![]() 大于80时学习效果最佳.
大于80时学习效果最佳.

(1)试求![]() 的函数关系式;
的函数关系式;
(2)教师在什么时段内安排核心内容,能使得学生学习效果最佳?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确说法的个数是( )
①在用![]() 列联表分析两个分类变量
列联表分析两个分类变量![]() 与
与![]() 之间的关系时,随机变量
之间的关系时,随机变量![]() 的观测值
的观测值![]() 越大,说明“
越大,说明“![]() 与
与![]() 有关系”的可信度越大
有关系”的可信度越大
②以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() 的值分别是
的值分别是![]() 和0. 3
和0. 3
③已知两个变量具有线性相关关系,其回归直线方程为![]() ,若
,若![]() ,
,![]() ,则
,则![]()
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
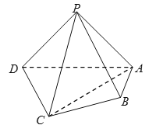
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若f(x)的图象上存在关于原点对称的点,则称f(x)为定义域上的“伪奇函数”.
(1)若f(x)=ln(2x+1)+m是定义在区间[﹣1,1]上的“伪奇函数”,求实数m的取值范围;
(2)试讨论f(x)=4x﹣m2x+2+4m2﹣3在R上是否为“伪奇函数”?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,
,![]() 在椭圆上,椭圆的左顶点为
在椭圆上,椭圆的左顶点为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 倍.
倍.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() (
(![]() )与椭圆
)与椭圆![]() 交于
交于![]() ,
,![]() ,连接
,连接![]() ,
,![]() 并延长交椭圆
并延长交椭圆![]() 于
于![]() ,
,![]() ,连接
,连接![]() ,指出
,指出![]() 与
与![]() 之间的关系,并说明理由.
之间的关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com