练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】执行如图所示的程序框图，则输出的S值是（ ）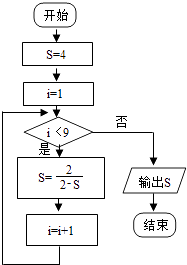

    A.﹣1
    B.
    C.
    D.4

    【答案】D
    【解析】解：第1次判断后循环，S=﹣1，i=2，
    第2次判断后循环，S= ，i=3，
    第3次判断后循环，S= ，i=4，
    第4次判断后循环，S=4，i=5，
    第5次判断后循环，S=﹣1，i=6，
    第6次判断后循环，S= ，i=7，
    第7次判断后循环，S= ，i=8，
    第8次判断后循环，S=4，i=9，
    第9次判断不满足9＜8，推出循环，输出4．
    故选D．

    【考点精析】通过灵活运用算法的循环结构，掌握在一些算法中，经常会出现从某处开始，按照一定条件，反复执行某一处理步骤的情况，这就是循环结构，循环结构可细分为两类：当型循环结构和直到型循环结构即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）= ，g（x）=ax2+bx（a，b∈R，a≠0）若y=f（x）的图象与y=g（x）图象有且仅有两个不同的公共点A（x1 ， y1），B（x2 ， y2），则下列判断正确的是（ ）
    A.当a＜0时，x1+x2＜0，y1+y2＞0
    B.当a＜0时，x1+x2＞0，y1+y2＜0
    C.当a＞0时，x1+x2＜0，y1+y2＜0
    D.当a＞0时，x1+x2＞0，y1+y2＞0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4―4：坐标系与参数方程]

    在直角坐标系xOy中，曲线C的参数方程为（θ为参数），直线l的参数方程为.

    （1）若a=1，求C与l的交点坐标；

    （2）若C上的点到l的距离的最大值为，求a.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为（为参数），直线的参数方程为（为参数）.

    （1）求和的直角坐标方程；

    （2）若曲线截直线所得线段的中点坐标为，求的斜率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a，b为常数，且a≠0，f(x)＝ax2＋bx，f(2)＝0，方程f(x)＝x有两个相等实数根．

    (1)求函数f(x)的解析式；

    (2)当x∈[1,2]时，求f(x)的值域；

    (3)若F(x)＝f(x)－f(－x)，试判断F(x)的奇偶性，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地铁换乘站设有编号为，，，，的五个安全出口.若同时开放其中的两个安全出口，疏散1000名乘客所需的时间如下：

    安全出口编号

    ，

    ，

    ，

    ，

    ，

    疏散乘客时间（）

    186

    125

    160

    175

    145

    则疏散乘客最快的一个安全出口的编号是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正三棱锥P﹣ABC，点P，A，B，C都在半径为 的球面上，若PA，PB，PC两两垂直，则球心到截面ABC的距离为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】二次函数在区间上有最大值4，最小值0.

    （1）求函数的解析式；

    （2）设，若在时恒成立，求的范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知复数z满足|z|= 的虚部为2，z所对应的点在第一象限，

    (1)求z;

    (2)若z,z2,z-z2在复平面上对应的点分别为A,B,C,求cos∠ABC.

    查看答案和解析>>

    同步练习册答案