
����Ŀ��ʹ��֧��������֧���Ѿ���Ϊ�������������Ҫ������֧����ʽ��ij����ͨ��ͳ�Ʒ���һ���ڳ���ÿ��ľ�����![]() (��Ԫ)��ÿ��ʹ��֧��������֧��������
(��Ԫ)��ÿ��ʹ��֧��������֧��������![]() (ǧ��)����������ع�ϵ�����õ����һ��
(ǧ��)����������ع�ϵ�����õ����һ��![]() ��7���������±�����������Ϊ��������.
��7���������±�����������Ϊ��������.

(1)����ɢ��ͼ��������ع鷽��![]() (
(![]() ��
��![]() ��ȷ��
��ȷ��![]() )��
)��

(2)����Ϊ�˴̼���һ���ѣ�������һ��չʹ��֧��������֧������齱����ܽ���7��Ԫ.�����г����飬�齱���ʹʹ��֧��������֧��������������7ǧ�ˣ��Ծ��߳����Ƿ��б�Ҫ��
չ�齱���
(3)���й��������:����һ�����գ����ڶ���ľ������ǰһ�������������ɣ����ȫ��Ա�����н�������(��)�ľ����£���ȫ��Ա�����������ý����ĸ���.
�����: ![]() ��
��![]() ��
��![]() ��
��![]() .
.
�ο���ʽ��![]() ��
�� ��
��![]() .
.
���𰸡���1��![]() ����2������������3��
����2������������3��![]()
��������
(1)ͨ��������㼴�ɣ��ȼ���![]() ��
��![]() ��Ȼ��ͨ����ʽ��������Իع鷽�̣�
��Ȼ��ͨ����ʽ��������Իع鷽�̣�
��2���ȼ�����չ��ʹ��֧��������֧��������Ϊ![]() (ǧ��)�����루1���ʵõ������
(ǧ��)�����루1���ʵõ������
��3�����ж���һ������ȫ��Ա��ֻ���ܶ������������ġ����ջ�ý������Ӷ�ȷ�������¼������ҳ����������ý����Ļ����¼����ʿɼ����ȫ��Ա�����������ý����ĸ���.
(1)ɢ��ͼ��ͼ��ʾ
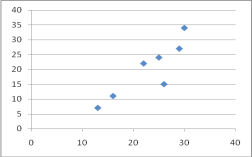
![]() ��
��![]()
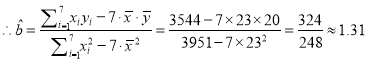
![]()
![]() ����
����![]() �Ļع鷽��Ϊ
�Ļع鷽��Ϊ![]()
(2)���չ��ʹ��֧��������֧��������Ϊ![]() (ǧ��)
(ǧ��)
��(1)�ã���![]() ʱ��
ʱ��![]()
��ʱ���еľ�����ԼΪ![]() ���ʳ����б�Ҫ��չ�齱�
���ʳ����б�Ҫ��չ�齱�
(3)����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�ʴ���һ������ȫ��Ա��ֻ���ܶ������������ġ����ջ�ý���
����һ���������������죬�����¼�Ϊ(��һ���ܶ�)��(�ܶ�������)��(����������)��(���ġ�����)��(���塢����)��(����������)����6�������¼�
���������ý����Ļ����¼�Ϊ(�ܶ�������)��(����������)����2�������¼�
��ȫ��Ա�����������ý����ĸ���Ϊ![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʷ�ǡ�����ʮ�塶���������д����塷��������һ���⣺�����������������ɵ��ϵ��������������е����������������ϵ�������ɵ��е��������������µ����������������е�������ɵ��µ��������������µ������ִ�˫������ƥ�����ѡһƥ������һ��������������ʤ�ĸ����ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij��ҵ������ij�ֲ�Ʒ�г�ȡ![]() ����������Щ��Ʒ��һ������ָ��ֵ���ɲ����������Ƶ�ʷֲ�ֱ��ͼ��
����������Щ��Ʒ��һ������ָ��ֵ���ɲ����������Ƶ�ʷֲ�ֱ��ͼ��
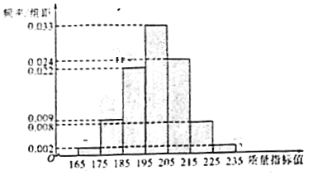
��1������![]() ����Ʒ����ָ��ֵ������ƽ����
����Ʒ����ָ��ֵ������ƽ����![]() ����������
����������![]() ��ͬһ���е������ø���������е�ֵ����������
��ͬһ���е������ø���������е�ֵ����������
��2����ֱ��ͼ������Ϊ�����ֲ�Ʒ������ָ��ֵ![]() ������̬�ֲ�
������̬�ֲ�![]() ������
������![]() ����Ϊ����ƽ����
����Ϊ����ƽ����![]() ��
��![]() ������������
������������![]() .
.
�����ø���̬�ֲ�����![]() ��
��
��ij�û��Ӹ���ҵ������![]() �����ֲ�Ʒ����
�����ֲ�Ʒ����![]() ��ʾ��
��ʾ��![]() ����Ʒ������ָ��ֵλ������
����Ʒ������ָ��ֵλ������![]() �IJ�Ʒ����.���âٵĽ������
�IJ�Ʒ����.���âٵĽ������![]() .
.
����![]() .��
.��![]() ����
����![]() ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=x��alnx+ ![]() ��
��
������a��1������f��x���ĵ������䣻
������a��3������g��x��=a2x2+3��������x1 �� x2��[ ![]() ��2]��ʹ��|f��x1����g��x2��|��9��������a��ȡֵ��Χ��
��2]��ʹ��|f��x1����g��x2��|��9��������a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��![]() �IJ������̣�
�IJ������̣�![]() ��
��![]() ������������
Ϊ������������![]() �IJ������̣�
�IJ������̣�![]() ��
��![]() Ϊ����������ֱ�߽�����
Ϊ����������ֱ�߽�����![]() ��
��![]() ��
��![]() ����.
����.
��������![]() �IJ������̻�Ϊ��ͨ���̣�����
�IJ������̻�Ϊ��ͨ���̣�����![]() ʱ��
ʱ��![]() �ij��ȣ�
�ij��ȣ�
���� ��֪��![]() ��
��![]() ����ֱ����б��
����ֱ����б��![]() �仯ʱ��
�仯ʱ��![]() �ķ�Χ.
�ķ�Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ǻ���![]() �IJ���ͼ��.
�IJ���ͼ��.

��1������![]() �ı���ʽ��
�ı���ʽ��
��2��������![]() ���㷽��
���㷽��![]() ������
������![]() �ڵ�����ʵ����֮�ͣ�
�ڵ�����ʵ����֮�ͣ�
��3���Ѻ���![]() ��ͼ�����������Ϊԭ����������Ȼ������ƽ��
��ͼ�����������Ϊԭ����������Ȼ������ƽ��![]() ����λ���ٰ��������쳤Ϊԭ�����������������ƽ��һ����λ�õ�����
����λ���ٰ��������쳤Ϊԭ�����������������ƽ��һ����λ�õ�����![]() ��ͼ�����������
��ͼ�����������![]() ������
������![]() ������
������![]() ��������һ���⣬������
��������һ���⣬������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڳ��оɳǸ����У�ijС��Ϊ��������ס����������С�������õ��й滮һ�����Ϊ![]() �ľ���������ͼ��ʾ�������滮Ҫ���ھ����ڵ����ܰ���
�ľ���������ͼ��ʾ�������滮Ҫ���ھ����ڵ����ܰ���![]() �����̻����̻����Ϊ200Ԫ/
�����̻����̻����Ϊ200Ԫ/![]() ���м��������Ӳ���Է�����ڷ��ø��ཡ�����ģ�Ӳ�����Ϊ100Ԫ/
���м��������Ӳ���Է�����ڷ��ø��ཡ�����ģ�Ӳ�����Ϊ100Ԫ/![]() .����εij�Ϊ
.����εij�Ϊ![]() .
.

��1���������![]() ��Ԫ����ʾΪ����
��Ԫ����ʾΪ����![]() �ĺ�����
�����
��2����![]() ȡ��ֵʱ���������ͣ��������������.
ȡ��ֵʱ���������ͣ��������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ΪԲ
ΪԲ![]() ��һ���㣬Բ��
��һ���㣬Բ��![]() ����
����![]() ��ĶԳƵ�Ϊ
��ĶԳƵ�Ϊ![]() ����
����![]() �ֱ����߶�
�ֱ����߶�![]() �ϵĵ㣬��
�ϵĵ㣬��![]() .
.
��1�����![]() �Ĺ켣���̣�
�Ĺ켣���̣�
��2��ֱ��![]() ���
���![]() �Ĺ켣
�Ĺ켣![]() ֻ��һ��������
ֻ��һ��������![]() ���ҵ�
���ҵ�![]() �ڵڶ����ޣ�������ԭ��
�ڵڶ����ޣ�������ԭ��![]() ����
����![]() ��ֱ��ֱ��
��ֱ��ֱ��![]() ��Բ
��Բ![]() �ཻ��
�ཻ��![]() ���㣬��
���㣬��![]() �����ȡֵ��Χ.
�����ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com