
| A. | $\sqrt{3}-1$ | B. | $\sqrt{3}+1$ | C. | $\frac{{\sqrt{3}+1}}{2}$ | D. | $\sqrt{3}+1$或$\frac{{\sqrt{3}+1}}{2}$ |
分析 利用正弦定理计算∠MF2F1=60°或120°,分类求出c的值,利用双曲线的定义计算a,即可求得双曲线的离心率.
解答 解:∵M是双曲线上的一点,|MF1|=$\sqrt{3}$,|MF2|=1,∠MF1F2=30°,
由正弦定理可得,$\frac{|M{F}_{2}|}{sin∠M{F}_{1}{F}_{2}}$=$\frac{|M{F}_{1}|}{sin∠M{F}_{2}{F}_{1}}$,即$\frac{1}{sin30°}$=$\frac{\sqrt{3}}{sin∠M{F}_{2}{F}_{1}}$,
解得sin∠MF2F1=$\frac{\sqrt{3}}{2}$,
∴∠MF2F1=60°或120°,
当∠MF2F1=60°时,△MF2F1为直角三角形,此时2c=|F2F1|=2.即c=1,
∵2a=|MF1|-MF2|=$\sqrt{3}$-1,即a=$\frac{\sqrt{3}-1}{2}$
∴e=$\frac{c}{a}$=$\sqrt{3}$+1,
当∠MF2F1=120°时,△MF2F1为直角三角形,此时2c=|F2F1|=|MF1|=1.即c=$\frac{1}{2}$,
∵2a=|MF1|-MF2|=$\sqrt{3}$-1,即a=$\frac{\sqrt{3}-1}{2}$,
∴e=$\frac{c}{a}$=$\frac{\frac{1}{2}}{\frac{\sqrt{3}-1}{2}}$=$\frac{\sqrt{3}+1}{2}$,
故选:D.
点评 本题考查双曲线的定义,考查双曲线的离心率,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | |x|≥1 | B. | |x+y|≥1 | C. | y≤-2 | D. | $|x|≥\frac{1}{2}$且$|y|≥\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 经过平面外一点有且只有一条直线与已知平面垂直 | |
| B. | 经过平面外一点有且只有一条直线与已知平面平行 | |
| C. | 经过平面外一点有且只有一条直线与已知直线垂直 | |
| D. | 经过平面外一点有且只有一平面与已知平面垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,4) | B. | [4,5) | C. | (-3,-2) | D. | (2,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
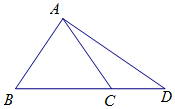 已知△ABC是等边三角形,D在BC的延长线上,且CD=2,${S_{△ABD}}=6\sqrt{3}$.
已知△ABC是等边三角形,D在BC的延长线上,且CD=2,${S_{△ABD}}=6\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com