
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若直线![]() 与曲线
与曲线![]() 的交点的横坐标为
的交点的横坐标为![]() ,且
,且![]() ,求整数
,求整数![]() 所有可能的值.
所有可能的值.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:
(1)求出导函数![]() ,根据
,根据![]() 的值分下、负、0进行讨论,可得
的值分下、负、0进行讨论,可得![]() 的正负,从而得单调性;
的正负,从而得单调性;
(2)![]() 即方程
即方程![]() 的解,由于
的解,由于![]() ,方程变形为
,方程变形为![]() ,这样只要研究函数
,这样只要研究函数![]() 的零点可能在哪个区间即可,由导数知
的零点可能在哪个区间即可,由导数知![]() 是
是![]() 和
和![]() 上的单调增函数,计算
上的单调增函数,计算![]() 可得结论.
可得结论.
试题解析:
(1)解: ![]() ,∴
,∴![]() ,
,
①若![]() 时,
时, ![]() 在
在![]() 上恒成立,所以函数
上恒成立,所以函数![]() 在
在![]() 上单调递增;
上单调递增;
②若![]() 时,当
时,当![]() 时,
时, ![]() ,函数
,函数![]() 单调递增,
单调递增,
当![]() 时,
时, ![]() ,函数
,函数![]() 单调递减;
单调递减;
③若![]() 时,当
时,当![]() 时,
时, ![]() ,函数
,函数![]() 单调递减,
单调递减,
当![]() 时,
时, ![]() ,函数
,函数![]() 单调递增.
单调递增.
综上,若![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
若![]() 时,函数
时,函数![]() 在
在![]() 内单调递减,在区间
内单调递减,在区间![]() 内单调递增;
内单调递增;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 内单调递增,在区间
内单调递增,在区间![]() 内单调递减,
内单调递减,
(2)由题可知,原命题等价于方程![]() 在
在![]() 上有解,
上有解,
由于![]() ,所以
,所以![]() 不是方程的解,
不是方程的解,
所以原方程等价于![]() ,令
,令![]() ,
,
因为![]() 对于
对于![]() 恒成立,
恒成立,
所以![]() 在
在![]() 和
和![]() 内单调递增.
内单调递增.
又![]() ,
,
所以直线![]() 与曲线
与曲线![]() 的交点有两个,
的交点有两个,
且两交点的横坐标分别在区间![]() 和
和![]() 内,
内,
所以整数![]() 的所有值为-3,1.
的所有值为-3,1.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:高中数学 来源: 题型:
【题目】已知以点C(t,![]() ) (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
) (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y﹣4=0与圆C交于点M、N,若OM=ON,求圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体中,四边形ABCD是矩形,平面ABCD⊥平面ABE,已知AB=2,AE=BE= ![]() ,且当规定正视图方向垂直平面ABCD时,该几何体的侧视图的面积为
,且当规定正视图方向垂直平面ABCD时,该几何体的侧视图的面积为 ![]() .若M,N分别是线段DE、CE上的动点,则AM+MN+NB的最小值为
.若M,N分别是线段DE、CE上的动点,则AM+MN+NB的最小值为 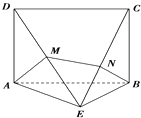
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有这样一则问题:“今有良马与弩马发长安,至齐,齐去长安三千里,良马初日行一百九十三里,日增一十三里;弩马初日行九十七里,日减半里,良马先至齐,复还迎弩马.”则现有如下说法:
①弩马第九日走了九十三里路;
②良马前五日共走了一千零九十五里路;
③良马和弩马相遇时,良马走了二十一日.
则以上说法错误的个数是( )个
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图四边形ABCD,AB=BD=DA=2.BC=CD= ![]() ,现将△ABD沿BD折起,使二面角A﹣BD﹣C的大小在[
,现将△ABD沿BD折起,使二面角A﹣BD﹣C的大小在[ ![]() ,
, ![]() ],则直线AB与CD所成角的余弦值取值范围是( )
],则直线AB与CD所成角的余弦值取值范围是( ) 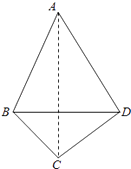
A.[0, ![]() ]∪(
]∪( ![]() ,1)
,1)
B.[ ![]() ,
, ![]() ]
]
C.[0, ![]() ]
]
D.[0, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且f(x)在(﹣∞,0]上单调递减,则不等式f(lgx)>f(﹣2)的解集是( )
A.( ![]() ,100)
,100)
B.(100,+∞)
C.( ![]() ,+∞)
,+∞)
D.(0, ![]() )∪(100,+∞)
)∪(100,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体P﹣ABCD中,平面ABCD⊥平面PAB,四边形ABCD为矩形,△PAB为正三角形,若AB=2,AD=1,E,F 分别为AC,BP中点. 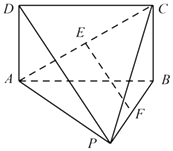
(Ⅰ)求证EF∥平面PCD;
(Ⅱ)求直线DP与平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为[﹣1,2],则函数g(x)=f(2x﹣ ![]() )的定义域为( )
)的定义域为( )
A.[ ![]() ,
, ![]() ]
]
B.[1, ![]() ]
]
C.[﹣1, ![]() ]
]
D.[﹣1, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2ax+3.
(1)若f(x)在(﹣∞, ![]() ]是减函数,在[
]是减函数,在[ ![]() ,+∞)是增函数,求函数f(x)在区间[﹣1,5]的最大值和最小值.
,+∞)是增函数,求函数f(x)在区间[﹣1,5]的最大值和最小值.
(2)求实数a的取值范围,使f(x)在区间[﹣5,5]上是单调函数,并指出相应的单调性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com