
【题目】(12分)
已知抛物线![]() 的焦点F与椭圆
的焦点F与椭圆![]() 的一个焦点重合,点
的一个焦点重合,点![]() 在抛物线上,过焦点F的直线l交抛物线于A,B两点.
在抛物线上,过焦点F的直线l交抛物线于A,B两点.
(1)求抛物线C的标准方程以及![]() 的值.
的值.
(2)记抛物线的准线![]() 轴交于点H,试问是否存在常数
轴交于点H,试问是否存在常数![]() ,使得
,使得![]() ,且
,且![]() 都成立.若存在,求出
都成立.若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
【题目】从1到7的7个数字中取两个偶数和三个奇数组成没有重复数字的五位数.
试问:(1)能组成多少个不同的五位偶数?
(2)五位数中,两个偶数排在一起的有几个?
(3)两个偶数不相邻且三个奇数也不相邻的五位数有几个?(所有结果均用数值表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,如图4①,②,③,④为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() (其中
(其中![]() )的部分图象如图所示,把函数
)的部分图象如图所示,把函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,再向下平移1个单位,得到函数
个单位长度,再向下平移1个单位,得到函数![]() 的图像.
的图像.

(1)当![]() 时,求
时,求![]() 的值域
的值域
(2)令![]() ,若对任意
,若对任意![]() 都有
都有![]() 恒成立,求
恒成立,求![]() 的最大值
的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)
已知函数![]() (a为实数).
(a为实数).
(1)当![]() 时,求函数
时,求函数![]() 的图像在
的图像在![]() 处的切线方程;
处的切线方程;
(2)求![]() 在区间
在区间![]() 上的最小值;
上的最小值;
(3)若存在两个不等实数![]() ,使方程
,使方程![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三角形的勃劳卡德点是以法国军官亨利·勃劳卡德(Henri.Brocard)命名的,他在1875年曾描述过这一事实,即:对任何一个三角形都存在唯一的角![]() ,即勃劳卡德角,使得图中连接三个顶点的线相交于勃劳卡德点Q,如图所示.
,即勃劳卡德角,使得图中连接三个顶点的线相交于勃劳卡德点Q,如图所示.
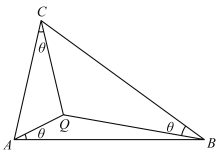
(1)研究发现:等腰直角三角形中![]() ,若
,若![]() 是斜边
是斜边![]() 的等腰直角三角形,求线段
的等腰直角三角形,求线段![]() 的长度;
的长度;
(2)若![]() 中,
中,![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若![]() 中,若线段
中,若线段![]() ,
,![]() ,
,![]() 的长度是1为首项,公比为q(
的长度是1为首项,公比为q(![]() )的等比数列,当
)的等比数列,当![]() 时,求公比q的值.
时,求公比q的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进行进价是每件10元,根据一周的销售数据得出周销售量![]() (件)与单价
(件)与单价![]() (元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
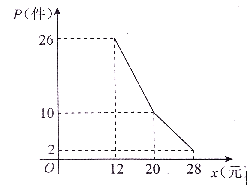
(1)根据周销售量图写出![]() (件)与单价
(件)与单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)写出利润![]() (元)与单价
(元)与单价![]() (元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com